NOIp 2020 赛前总结
近期考试情况
- 2020.11.14 230/400pts Rank 13/37 NOIp2020摸底测一试
self test on Luogu - 2020.11.15 172/400pts Rank 18/36 NOIp2020摸底测二试
self test on Lemonlime - 2020.11.21 56/400pts Rank 15/40 NOIp模拟
- 2020.11.21 94/100pts Rank 10/20 基本功
- 2020.11.22 80/400pts Rank 33/46 NOIp模拟
- 2020.11.22 72/100pts Rank 2/20 基本功
- 2020.11.23 179/400pts Rank 21/35 NOIp模拟 By 张乐天
- 2020.11.24 20/400pts Rank 16/27 NOIp模拟
- 2020.11.25 135/400pts Rank 9/26 倍增
- 2020.11.26 205/400pts Rank 2/25 NOIp模拟
- 2020.11.27 115/400pts Rank 12/25 NOIp模拟
- 2020.11.27 69/100pts Rank 14/25 基本功
- 2020.11.28 136/400pts Rank 12/37 NOIp模拟 By Fuyuki
- 2020.11.28 80/400pts Rank 23/36 NOIp模拟 By xzx34
- 2020.11.29 20/100pts Rank 16/23 基本功 - 算法片段
- 2020.11.30 50/400pts Rank 24/37 NOIp模拟 By 朱老师
- 2020.12.1 30/400pts Rank 24/35 NOIp模拟 By Yukikaze_
- 2020.12.2 255/400pts Rank 10/25 NOIp模拟
- 2020.12.3 145/400pts Rank 3/22 NOIp模拟
总结
考的很拉垮。
有时候做题策略不当,把时间大量投入在一道题目中,这样就可能会丢掉其他题目的部分分。
然后就是各种下饭错误,各种不取模,$MLE$。其实说到底是时间分配的不好,有的题太匆忙,可能甚至没跑大样例,细节上就会出错。
在接下来的$NOIp$中,要注意合理分配时间,每题拿暴力分,大胆猜想小心求证。
要开long long!
比赛总结
$CSP-S$之后,还是认真打洛谷月赛和$CodeForces$了,个人认为确实很有好处,能够见到很多精妙的题目,锻炼思维。
当然比较难受的是最近那场洛谷月赛因为大量$Special Judge$和交互题达成了史上对评测姬杀伤力最大的洛谷月赛成就。
算法总结
这一个板块,主要用来总结一些我接触过的算法,便于我进行复习。
搜索
搜索,就是对状态进行枚举,通过枚举所有的可能情况来找到最优解,或者统计合法解的个数。
搜索应该是最常用的算法之一,搜索能够帮我们拿到题目中的部分分,在经过优化和改良后,也是许多高级算法的基础,所以,这一个部分非常重要。
DFS
深度优先搜索($DFS$,$Depth \space First \space Search$)。$DFS$原本是图论中的算法,在搜索中,其实就是在搜索树上跑$DFS$,只要可能,就尽可能拓展当前情况,直到由当前情况拓展出的所有情况都被搜到为之。
代码层面上,$DFS$一般通过递归实现。
BFS
广度优先搜索($BFS$,$Breadth \space First \space Search$)。同样,广搜原本也是图论中的算法,他是$Prim$和$Dijkstra$算法的基础。
在搜索中,广搜体现为优先拓展搜索树上深度较低的结点,感性上理解广搜,就是一层一层进行搜索。
由于广搜的这一特点,广搜通常用来寻找一个问题的最优解。
代码上,广搜一般使用队列实现。
双向搜索
双向搜索通常是基于$BFS$的,从初始状态$startState$和目标状态$boundaryState$同时开始搜索,如果发现从其中一者拓展出的状态已经被另一者标记为$visited$,那么我们就认为已经找到了合法解。
普通搜索的搜索树是这样的:
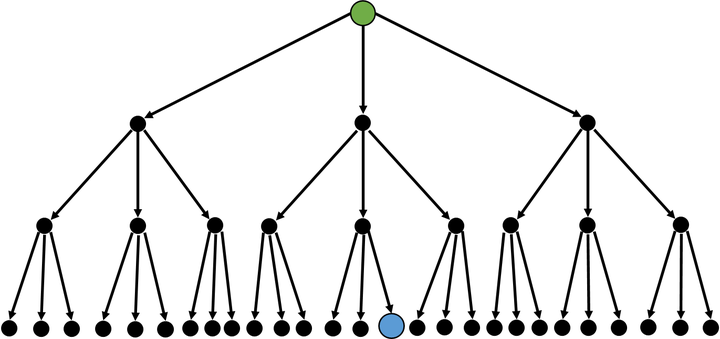
此时的时间复杂度,我们设为$O(n^k)$。
而如果使用双向搜索,效率上就会有所提高:在这到题目中
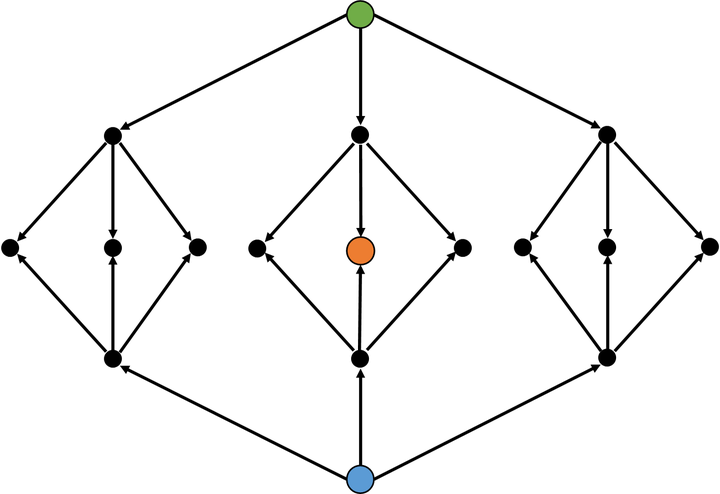
这个时候,我们的时间复杂度就优化至了$O(n^{k/2})$。
A*
A* 搜索算法(A* Search Algorithm)。首先我们引入估价函数$f(x)$,其作用是对状态进行估价,从而选取更优解或是删除无效解,可行性剪枝和最优性剪枝其实也就是对当前状态进行了估价。A*算法提供了一种设计估价函数的方式,并且以此优化了广搜。
在A*中,除了估价函数$f(x)$,我们另外引入两个函数:
- $g(x)$:从初始状态到当前状态的代价
- $h(x)$:从当前状态到目标状态的代价
那么此时,$f(x)=g(x)+h(x)$。你可以发现,双向搜索也可以用A*来解释。
$A^ *$的核心在于如何设计$h(x)$,因为这是未知的,如果能将实际问题转化为A*的模型,那么A*的实现也非常简单,将$BFS$中的队列改为优先队列即可。
接下来,看一道简单题,理解一下A*建模的过程。Luogu P4667 [SCOI2007]k短路
在这到题目中,我们首先以$a$为源点跑一次单源最短路,接下来,我们来设计$g(x)$和$h(x)$:
- $g(x)=\delta(a,x)$
- $h(x)=\delta(x,b)$
其中,$\delta(u,v)$指结点$u$到结点$v$的最短路径权重。
这样,k短路问题就被转化为了标准的A*模型。
#include<bits/stdc++.h>
#define File(name) freopen(name".in", "r", stdin); freopen(name".out", "w", stdout);
#define Int inline int
#define Void inline void
#define Bool inline bool
#define DB inline double
#define LL inline long long
#define ri register int
#define re register
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef double db;
int n, m, k, a, b, u, v, l, cnt, dst[55];
bool vis[55];
struct edge{
int v, w;
edge() {}
edge(int v, int w): v(v), w(w) {}
};
vector<edge> g[55];
vector<edge> G[55];
struct node{
int pos, dis;
node() {}
node(int pos, int dis): pos(pos), dis(dis) {}
Bool operator < (const node &b) const{
return dis > b.dis;
}
};
priority_queue<node> q;
struct data{
int pos, pass;
vector<int> step;
data() {}
data(int pos, int pass, vector<int> step): pos(pos), pass(pass), step(step) {}
Bool operator < (const data &b) const{
if(pass + dst[pos] != b.pass + dst[b.pos]) return pass + dst[pos] > b.pass + dst[b.pos];
// if(step.size() != b.step.size()) return step.size() > b.step.size();
for(ri i = 0; i < step.size(); i++) if(step[i] != b.step[i]) return step[i] > b.step[i];
}
};
priority_queue<data> Q;
LL read(){
ll n = 0; int f = 1; char ch = getchar();
while('0' > ch || ch > '9'){
if(ch == '-') f *= -1;
ch = getchar();
}
while('0' <= ch && ch <= '9'){
n = (n << 1) + (n << 3) + ch-'0';
ch = getchar();
}
return f * n;
}
Void write(ll x){
if(x/10) write(x/10);
putchar(x%10+'0');
}
Void input() {}
template<typename Type, typename... Types>
Void input(Type& arg, Types&... args){
arg = read();
input(args...);
}
Void Dijkstra(){
for(ri i = 1; i <= n; i++) dst[i] = 0x7fffffff;
dst[b] = 0;
q.push(node(b, 0));
while(!q.empty()){
node now = q.top();
q.pop();
if(vis[now.pos]) continue;
vis[now.pos] = true;
for(auto x: g[now.pos]){
if(vis[x.v]) continue;
if(dst[x.v] > dst[now.pos] + x.w){
dst[x.v] = dst[now.pos] + x.w;
q.push(node(x.v, dst[x.v]));
}
}
}
}
Void Astar(){
Q.push(data(a, 0, {a}));
while(!Q.empty()){
data now = Q.top();
Q.pop();
if(now.pos == b){
cnt++;
// cout << ">>>>> ";
// for(ri i = 0; i < now.step.size()-1; i++) write(now.step[i]), putchar('-');
// write(now.step[now.step.size()-1]);
// cout << endl;
if(cnt == k){
for(ri i = 0; i < now.step.size()-1; i++) write(now.step[i]), putchar('-');
write(now.step[now.step.size()-1]);
exit(0);
}
continue;
}
for(auto x: G[now.pos]){
bool flag = false;
for(auto y: now.step) if(y == x.v) { flag = true; break; }
if(flag) continue;
vector<int> tmp;
tmp = now.step;
tmp.push_back(x.v);
Q.push(data(x.v, now.pass+x.w, tmp));
}
}
}
int main(){
input(n, m, k, a, b);
if(n == 30 && m == 759){
puts("1-3-10-26-2-30");
return 0;
}
for(ri i = 0; i < m; i++){
input(u, v, l);
g[v].push_back(edge(u, l));
G[u].push_back(edge(v, l));
}
Dijkstra();
Astar();
puts("No");
return 0;
}IDA*
启发式迭代加深($IDA^ *$,$Iterative \ Deepening \ A^ *$)。迭代加深非常简单,即每次给$DFS$添加一个深度限制,只要当前状态在搜索树上的深度超过了限制,就直接剪枝。但是这里注意,每次$depthLimit$增加时,迭代加深搜索都会重新从起点开始搜索,这样,深度较低的结点会被搜索多次,所以,迭代加深搜索的效率并不高。迭代加深搜索仅适用于搜索树深度极大,但我们能够确定在深度较低的位置存在着合法解的情况。
这里所说的$IDA^ *$是在迭代加深搜索中引入了$A^ *$中的估价函数$f(x)$,$IDA^ *$中,$g(x)$是当前深度,$h(x)$是乐观估计当前状态还需要拓展多少层才能找到合法解。
考虑埃及分数这道$IDA^ *$例题,在这到题目中,搜索树理论上是无限大的,不可能是用普通的$DFS$或$BFS$解决,那么我们可以考虑使用$IDA^ *$。我们强制要求搜索时分数大小是不上升的,那么,就可以用他来设计$h(x)$,一旦$g(x)+h(x)>depthLimit$就剪枝。这就是一个非常标准的$IDA^ *$模型。
搜索部分小结
在比赛中,遇到一道较难的题目,我们通常可以轻松通过暴力搜索拿到第一档部分分,如果我们通过一些高级搜索算法对暴搜进行优化,就可能能够拿到一个非常优秀的成绩,甚至通过某些玄学剪枝$AC$。练好搜索在现阶段非常重要
DP
动态规划($DP$,$Dynamic \ Programming$)。动规在联赛中所占的比重非常大,但同时难度也非常大:一方面,动规的题型非常多,想熟练掌握基础的动规难度就很大,另一方面,动规的思想极其巧妙,在某些题目中,难以搭建动态规划模型。
背包
背包$DP$是动态规划中一个比较复杂的分支,此处总结各类背包的一般性解法。
01背包
每个物品只有两种状态,选&不选,这种背包问题称作01背包。
共$n$个物品,背包容量为$W$,第$i$个物品的价值为$v_i$,重量为$w_i$,每个物品仅$1$件。
首先考虑设$dp_{i,j}$表示在前$i$个物品放在容量为$j$的背包内能够获得的最大价值。
转移方程显而易见:$dp_{i,j}=max\{dp_{i-1,j},dp_{i-1,j-w_i}+v_i\}$。
发现$dp_i$只会被$dp_{i-1}$影响,那么我们压掉$dp$的第一维,使用滚动数组节省空间。
$$
dp_{i}=max\{dp_{i},dp_{i-w_i}+v_i\}
$$
for(int i = 1; i <= n; i++)
for(int j = W; j >= w[i]; j--)
dp[j] = max(dp[j], dp[j-w[i]] + v[i]);时间复杂度是$O(nW)$的。
完全背包
与01背包不同的地方在于,完全背包内的物品可以选择多次。
共$n$个物品,背包容量为$W$,第$i$个物品的价值为$v_i$,重量为$w_i$,每个物品有无数件。
考虑朴素的转移:$dp_i=max^{+\infin}_{k=0}\{dp_{i-kw_i}+kv_i\}$。
裂开了。
考虑怎么进行简单的优化,我们完全可以将转移方程写成这样:$dp_{i}=max\{dp_{i},dp_{i-w_i}+v_i\}$,原因是,转移$dp_i$之前,$dp_{i-w_i}$已经从$dp_{i-2w_i}$转移过了,以此类推。
值得注意的是,此时我们的代码中,第二个循环需要改一下,因为我们在转移$dp_i$时需要$dp_{i-w_i}$的结果。
for(int i = 1; i <= n; i++)
for(int j = w[i]; j <= W; j++)
dp[j] = max(dp[j], dp[j-w[i]] + v[i]);时间复杂度$O(nW)$。
多重背包
和01背包和完全背包不同的地方在于,多重背包中每个物品有$k_i$件。
共$n$个物品,背包容量为$W$,第$i$个物品的价值为$v_i$,重量为$w_i$,每个物品有$k_i$件。
同样先考虑朴素的转移:$dp_i=max^{k_i}_{k=0}\{dp_{i-kw_i}+kv_i\}$。
时间复杂度$O(nW\sum k_i)$。
优化也非常好想,我们将$k_i$个物品分成$2^j(j\in Z)$份,然后转化为01背包问题解决即可。
现在的复杂度是$O(nW\sum \log_2k_i)$。
分组背包
分组背包,即将物品分组后,每组物品只能选出一个。
要想解决分组背包问题,我们首先考虑01背包的思想,即每次在所有物品中选择一个,分组背包中,我们每次要从一组中选出一个,所以我们只需要对每一组做一次01背包即可。
for each group in groups as k:
for each element in k as i:
for j: W -> 0:
dp[j] = max(dp[j], dp[j-w[i]]+v[i])$Pseudo \ Code \ From$ 背包九讲($Modified$)
树形依赖背包
这种背包问题最初起源于2006 NOIp提高 金明的预算方案这一问题,这道题就是一个简单的树形依赖背包,我们首先从这里入手。
在本体中,主件和附件有一个特点:
每个主件可以有$0$个、$1$个或$2$个附件。
每个附件对应一个主件,附件不再有从属于自己的附件。
根据这一特性,我们就可以设计转移:
- 不选
- 选主件
- 选主件和附件1(如果存在)
- 选主件和附件2(如果存在)
- 选主件和附件1、2(如果存在)
五种情况分别讨论,那么这题就被转换为了01背包,很好解决。
#include<bits/stdc++.h>
//#define DEBUG
using namespace std;
struct object{
int v, w;
object(int vv = 0, int ww = 0): v(vv), w(ww) {}
};
object mainObject[32005], annexObject[32005][2];
int n, m, v, p, q, dp[32005];
int main(){
cin >> n >> m;
for(int i = 1; i <= m; i++){
cin >> v >> p >> q;
if(q == 0) mainObject[i] = object(v, v*p);
else if(annexObject[q][0].w == 0) annexObject[q][0] = object(v, v*p);
else annexObject[q][1] = object(v, v*p);
}
for(int i = 1; i <= m; i++) for(int j = n; mainObject[i].w != 0 && j >= mainObject[i].v; j--){
dp[j] = max(dp[j], dp[j-mainObject[i].v]+mainObject[i].w);
if(j >= mainObject[i].v + annexObject[i][0].v)
dp[j] = max(dp[j], dp[j-mainObject[i].v-annexObject[i][0].v]+mainObject[i].w+annexObject[i][0].w);
if(j >= mainObject[i].v + annexObject[i][1].v)
dp[j] = max(dp[j], dp[j-mainObject[i].v-annexObject[i][1].v]+mainObject[i].w+annexObject[i][1].w);
if(j >= mainObject[i].v + annexObject[i][0].v + annexObject[i][1].v)
dp[j] = max(dp[j], dp[j-mainObject[i].v-annexObject[i][0].v-annexObject[i][1].v]+mainObject[i].w+annexObject[i][0].w+annexObject[i][1].w);
}
#ifndef DEBUG
cout << dp[n];
#else
for(int i = 0; i <= n; i++) cout << dp[i] << " ";
#endif
return 0;
}那么问题来了,如果附件还有附件,此时问题将不能简单地通过分类讨论解决,因为依赖关系是树形结构的,非常复杂。
此时,我们就需要将背包的思想运用到树形$DP$中。对于CTSC1997 选课这题来说,其核心代码如下:
void dfs(int now){
for(auto x: g[now]){
dfs(x);
for(int i = m + 1; j >= 1; j--)
for(int j = 0; j < i; j++)
dp[now][i] = max(dp[now][i], dp[x][j] + dp[now][i-j]);
}
}泛化物品
泛化物品的背包可以说是背包问题形式化的描述。
在泛化中,物品的重量和价值并不固定给出,而是对于一件物品$i$,若其价值为$v_i$,则其重量为$h(v_i)$。
应该说,泛化物品是一种思想,一个背包问题会给出物品的属性,物品之间的依赖关系等等,但一定能够将其对应为某件泛化物品。
非常玄学。
我想说:“思考”是一个$OIer$最重要的品质。简单的问题,深入思考以后,也能发现更多。
——《背包九讲》
背包部分小结
一定要将背包的思想真正理解,要不然,只要题目稍加包装,你就看不出这是一道背包题了。
看一道题:
2014 NOIp提高 飞扬的小鸟
小鸟每个单位时间沿横坐标方向右移的距离为$1$,竖直移动的距离由玩家控制。如果点击屏幕,小鸟就会上升一定高度$x$,每个单位时间可以点击多次,效果叠加;如果不点击屏幕,小鸟就会下降一定高度$y$。小鸟位于横坐标方向不同位置时,上升的高度$x$和下降的高度$y$可能互不相同。
当时我模拟赛考过这一题,直接暴搜模拟,似乎拿了$10pts$的部分分(?),其实现在看起来,很容易想到这是多重背包问题:上升对应完全背包,下降对应01背包。
所以说,思考和理解很重要。
但是把板子记牢也很重要,背包的题型很多,要是看出了一道题是背包但是不会打就离谱……
数位DP
数位$DP$已经不是我第一次在模拟赛中遇到了,所以得简单写写,是个很重要的东西。
数位$DP$题的一般形式,都是给出了一个区间$[l,r]$,询问区间中有多少个$x$满足条件$f(x)$。
其中,$f$通常是数字层面的某种性质,比如:
不含前导$0$且相邻两个数字相差至少为$2$。($windy$数)
存在长度至少为2的回文子串(萌数)
解法上,通常通过$ans_r-ans_{l-1}$计算答案。
其实数位$DP$题都比较类似,做多了就能找到规律。数字组成的奥妙——数位dp这篇文章描述了数位$DP$中很多细节。
此处我们考虑上面提到过的$windy$数应该怎么转移,其实很好想,设$dp_{i,j}$表示长度为$i$,最高位为$j$的$windy$数个数,有转移方程:
$$
dp_{i,j}=\sum dp_{i-1,k}(|k-j|\geq 2)
$$
基本上,数位$DP$就是这样了。
DP部分小结
简单的$DP$题很简单,但是想要把$DP$题出难就难得离谱,$DP$其实就是递推,其变式多的离谱,想要较为熟练的掌握,确实是个较为长期的过程。
考试的时候,应该考虑用记忆化优化暴力搜索,目前来看,这样可行性更高。
图论
图的存储
考虑这样一个图:
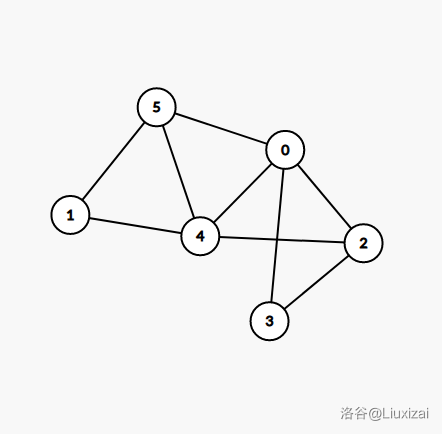
邻接矩阵
在结点数较少的时候适用,因为其空间复杂度是严格$O(N^2)$的。
$$
G= \begin{pmatrix}
0 & +\infin & 1 & 1 & 1 & 1 \\
+\infin & 0 & +\infin & +\infin & 1 & 1 \\
1 & +\infin & 0 & 1 & 1 & +\infin \\
1 & +\infin & 1 & 0 & +\infin & +\infin \\
1 & 1 & 1 & +\infin & 0 & 1 \\
1 & 1 & +\infin & +\infin & 1 & 0
\end{pmatrix}
$$
STL Vector
这应该是最实用的存图方式(大概)。
其基于邻接表,空间复杂度是$O(E)$的。
$$
\begin{aligned}
G_0 & =\{2,4,5\} \\
G_1 & =\{4,5\} \\
G_2 & =\{0,3,4\} \\
G_3 & =\{0,2\} \\
G_4 & =\{0,1,2,5\} \\
G_5 & =\{0,1,4\}
\end{aligned}
$$
这样存图有个好处,可以使用C++11中自动迭代器进行遍历:
for(auto x: G[k]):
// ...可能会慢一点,但通常可以用,主要是好写。
一般我都用Vector代替链式前向星(我好像就只在刚开始学图的时候写过一次链式前向星(?))。
最短路
Dijkstra
解决单源最短路径问题,适用于无负权的图。其算法核心是贪心。
肯定要随手加一个priority_queue,堆优化。
裸的$Dijkstra$复杂度是$O(n^2)$,但使用priority_queue优化后,能够达到$O(m \log m)$
int s;
int dst[N];
bool vis[N];
struct edge{
int v, w;
edge() {}
edge(int v, int w): v(v), w(w) {}
};
vector<edge> g[N];
struct node{
int pos, dis;
node() {}
node(int pos, int dis): pos(pos), dis(dis) {}
bool operator < (const node &b) const{
return dis > b.dis;
}
};
priority_queue<node> q;
void Dijkstra(){
for(int i = 1; i <= n; i++) dst[i] = 0x7fffffff;
dst[s] = 0;
q.push(node(s, 0));
while(!q.empty()){
node now = q.top();
q.pop();
if(vis[now.pos]) continue;
vis[now.pos] = true;
for(auto x: g[now.pos]){
if(vis[x.v]) continue;
if(dst[x.v] > dst[now.pos] + x.w){
dst[x.v] = dst[now.pos] + x.w;
q.push(node(x.v, dst[x.v]));
}
}
}
}Floyd
解决全源最短路径。其算法核心是$DP$。
复杂度是严格的$O(n^3)$。
int n;
int g[N][N];
void Floyd(){
for(int k = 0; k < n; k++)
for(int i = 0; i < n; i++)
for(int j = 0; j < n; j++)
g[i][j] = min(g[i][j], g[i][k]+g[k][j]);
}SPFA
关于$SPFA$,他死了。
$SPFA$,$Shortest \ Path \ Faster \ Algorithm$。这是$Bellman-Ford$算法的队列优化版本,在国内$OI$界曾十分流行:
2018 年 7 月 19 日,某位同学在 NOI Day 1 T1 归程 一题里非常熟练地使用了一个广为人知的算法求最短路。
然后呢?
$100 \rightarrow 60$;
$\text{Ag} \rightarrow \text{Cu}$;
最终,他因此没能与理想的大学达成契约。
原因是,$SPFA$的最劣时间复杂度能够达到$O(nm)$,基本上所有图论题都会卡$SPFA$,方法也非常简单,构造一个网格图,$SPFA$就跑不动了。
当然$SPFA$还是得学,因为$SPFA$一个很重要的功能是判负环。
$SPFA$解决单源最短路径。
复杂度已经提过了,其算法核心是$Relax$。
int s;
int dst[N];
bool inQueue[N];
struct node{
int v, w;
node() {}
node(int u, int v, int w): u(u), v(v), w(w) {}
};
vector<node> g[N];
queue<int> q;
void SPFA(){
q.push(s);
inQueue[s] = true;
while(!q.empty()){
int now = q.front();
q.pop();
inQueue[now] = false;
for(auto x: g[s]){
dst[x.v] = min(dst[x.v], dst[now]+x.w);
if(!inQueue[x.v]){
q.push(x.v);
inQueue[x.v] = true;
}
}
}
}判负环
很容易,我们给每个点加上属性$cnt$,表示该点被经过的次数,若图中无负环,则一条最短路径上最多经过了$n$个结点,换言之,一个点最多被经过了$n$次,如果$cnt > n$,那么我们就可以认定为图中有负环。
Johnson
解决全源最短路径。
考虑$Dijkstra$如何解决全源最短路,自然是以每个点为源点跑一次$Dijkstra$,复杂度是$O(nm \log m)$,比$Floyd$的$O(n^3)$更优,但问题在于$Dijkstra$无法在带负权的图上跑,$Johnson$算法就是在解决这一问题。
其算法核心是,首先建立0号结点,向每个结点连一条权值为0的边,以0号结点为源点跑一次$SPFA$。现在,记0号结点到结点$i$的最短路径是$dst_i$,那么,对于一条$u \rightarrow v$的边,若其权值为$w$,我们把他修改为$w+dst_u-dst_v$,使其权值不为负。
实质上,在此处,$dst$为势能。
接下来以每个结点为源点跑$Dijkstra$就行了,总复杂度仍然是$O(nm \log m)$。
SCC
强连通分量($SCC$,$Strongly \ Connected \ Components$)。
首先注意$dfs$生成树:

其中,有四种边:
- 树边,绿色边,即从一个结点前往另一个没有访问过的结点。
- 反祖边,黄色边,即从一个结点前往自己的祖先。
- 前向边,蓝色边,即从一个结点前往自己子树中的结点。
- 横叉边,红色边,即从一个结点前往另一个已被访问过的结点,且该结点并不是由当前结点的祖先拓展出来的。
有如下结论:
如果结点$u$是某个强连通分量在搜索树中遇到的第一个结点,那么这个强连通分量的其余结点肯定是在搜索树中以$u$为根的子树中。
简述证明过程。如果结点$v$和结点$u$在同一强连通分量中,且$v$不在$u$的子树中,那么$u \rightarrow v$一定是反祖边或横叉边,但在这两种情况下,$v$都在$u$之前被访问,于是矛盾。$\cal Q.E.D.$
Tarjan
$Tarjan$,可用于求强连通分量。
复杂度$O(n+m)$。
- $dfn$,时间戳,结点在$dfs$时被搜索到的时间
- $low$,追溯值,够追溯到的最早的栈中节点的次序号
- $stack$,栈
- $scc$,结点所属的强连通分量序号
int weight[10005], dfn[10005], low[10005], dfnCnt, stack[10005], top = -1, scc[10005], sc, w[10005];
bool inStack[10005], vis[10005];
vector<int> g[10005];
Void tarjan(int now){
dfn[now] = low[now] = ++dfnCnt;
stack[++top] = now; inStack[now] = true;
for(auto x: g[now]){
if(!dfn[x]){
tarjan(x);
low[now] = min(low[now], low[x]);
}
else if(inStack[x]){
low[now] = min(low[now], dfn[x]);
}
}
if(low[now] == dfn[now]){
sc++;
while(true){
int tmp = stack[top];
top--;
inStack[tmp] = false;
scc[tmp] = sc;
w[sc] += weight[tmp];
if(tmp == now) break;
}
}
}割点和桥
$Tarjan$稍微做一些修改就能求割点和桥。
割点:在图中删掉该点后,强连通分量数量会增加。
桥:在图中删掉该边后,强连通分量数量会增加。
求割点或割边时,对于所有$now\rightarrow v$,分两种情况:
-
dfn[v] == 0,$v$还未被访问过。此时,我们通过
low[now] = min(low[now], low[i]);操作更新追溯值。 -
dfn[v] != 0 and v != father,$v$曾被访问过,但$v$不是$now$的祖先。此时,我们通过
low[now] = min(low[now], dfn[i]);操作更新追溯值。
得到追溯值后,对于割点,我们的判定标准是$low_v \geq dfn_{now}$,割边就是$low_v > dfn_{now}$。
最小生成树
瓶颈生成树
- 定义:若$G$的一个生成树中最大边权在$G$的所有生成树中最小,我们称其为$G$的瓶颈生成树。
- 性质:最小生成树是瓶颈生成树的充分不必要条件,反证即可。
最小瓶颈路
-
定义:若$G$中一条$u \rightarrow v$路径上的最大边权在所有$u \rightarrow v$的简单路径中最小,则称其为$u \rightarrow v$的最小瓶颈路。
-
性质:最小生成树上$u \rightarrow v$的路径一定是$u \rightarrow v$的最小瓶颈路,由最小生成树的定义可推出。
最小生成树不唯一,但是每种最小生成树$u$到$v$路径的最大边权相同且为最小值。
二分图
二分图,$Bipartite \ Graph$,指一张图,其能够被分为两个部分,相同部分的点不会互相连边。
性质:二分图不存在奇环。
原因很简单,对二分图进行黑白染色后,任意一条边两端点的颜色一定不同,而对于奇环,无法满足这一条件。
二分图最大匹配
常用的是匈牙利算法。Luogu P3386 【模板】二分图最大匹配
#include<bits/stdc++.h>
using namespace std;
int n, m, e, u, v, ans, match[505];
bool g[505][505], vis[505];
inline bool dfs(int u){
for(int i = 1; i <= m; i++){
if(!vis[i] && g[u][i]){
vis[i] = true;
if(match[i] == 0 || dfs(match[i])){
match[i] = u;
return true;
}
}
}
return false;
}
int main(){
cin >> n >> m >> e;
for(int i = 0; i < e; i++){
cin >> u >> v;
g[u][v] = true;
}
for(int i = 1; i <= n; i++){
memset(vis, 0, sizeof(vis));
if(dfs(i)) ans++;
}
cout << ans;
return 0;
}其算法流程是:
- 向对面连边
- 如果这条边已经被连了,则向连这条边的结点发出换条边连的请求
- 如果这个点已经无边可连,驳回请求
- 当前点尝试其他的边,如果无边可连,就只能不连
复杂度是$O(nm)$的,如果将二分图转化为网络流模型,使用$Dinic$求解,复杂度可以优化至$O(\sqrt nm)$。暂时不会,以后学(Flag)。
图论部分小结
说实话我图论掌握的不好,很多板子打的不熟。
联赛之前争取熟练模板,联赛之后,重点学一下树上问题。
数学
Euler's Totient Function
欧拉函数,即$\varphi(x)$,表示小于等于$n$且与$n$互质的数的个数。
性质:
-
若$p$为质数,$\varphi(p)=\varphi(p-1)+1$,由定义。
-
若$n=p^k(k\in Z)$,$p$为质数,$\varphi(n) = p^k-p^{k-1}$,由定义。
-
$\varphi(xy)=\varphi(x)\varphi(y)$,由定义。
-
根据唯一分解定理,有$n=\prod\limits^s_{i=1}p_i^{k_i}$,那么
$$
\begin{aligned}
\varphi(n) & = \prod\limits^s_{i=1}\varphi(p_i^{k_i}) \\
& = \prod\limits^s_{i=1}(p_i^{k_i}-p_i^{k_{i-1}}) \\
& = \prod\limits^s_{i=1}p_i^{k_i}(1-\frac{1}{p_i}) \\
& = n \prod\limits^s_{i=1}\frac{p_i-1}{p_i}
\end{aligned}
$$
Modular Multiplicative Inverse
模意义下的乘法逆元,主要用于除法取模。
首先,什么是逆元:
$ax\equiv 1 \pmod b$的解被称为$a \ mod \ b$的逆元,记作$a^{-1}$。
快速幂法
$$
ax\equiv 1 \pmod b
$$
由费马小定理(若$p$为素数,$a^{p-1}\equiv 1 \pmod p$),有
$$
ax \equiv a^{b-1} \pmod b \\
x \equiv a^{b-2} \pmod b
$$
于是就可以用快速幂解决。
线性求逆元
$$
\begin{aligned}
& a = \lfloor \frac{p}{x} \rfloor \ \ \ \ b = p \ mod \ x \\
\implies & ax+b=p \\
\implies & ax+b \equiv 0 \pmod p \\
\implies & ab^{-1}+x^{-1} \equiv 0 \pmod p \\
\implies & x^{-1} \equiv -ab^{-1} \pmod p \\
\implies & x^{-1} \equiv -\lfloor \frac{p}{x} \rfloor (p\ mod\ x)^{-1} \pmod p
\end{aligned}
$$
此时注意到$p \ mod \ x < x$,那么,我们可以用严格$O(n)$的时间推出$1 \rightarrow n$的逆元。
如果我们需要求任意$n$个数的逆元。首先注意到逆元能够抵消,即$a^{-1} \times a=1$,那么,对于任意$n$个数$a_1,a_2,a_3...a_n$,我们这样进行操作:
$$
\begin{aligned}
S_i & = \prod\limits^i_{k=1}a_k \\
sv_i & = S_i^{-1} \\
sv_n & = p^{S_n-2}\ mod\ p \\
sv_i & = sv_{i+1} \times a_{i+1} \\
inv_i & = a_i^{-1} \\
inv_i & = sv_{i}\times s_{i-1}
\end{aligned}
$$
那么,这个算法的复杂度就是$O(n+\log p)$的,可以直接记成$O(n)$。
Lucas
$Lucas$定理用于求解大组合数取模的问题,其中$p$必须为素数。
$$
C_n^m=C_{\lfloor n/p\rfloor}^{\lfloor m/p \rfloor}\times C_{n \ mod \ p}^{m\ mod\ p}\pmod p
$$
Matrix
首先是最基础的矩阵乘法,对于一个$P\times M$的矩阵$A$和一个$M\times Q$的矩阵$B$,那么$A\times B$能够得到一个$P\times Q$的矩阵$C$。
对于$C$中的每一个元素:$C_{i,j}=\sum\limits^M_{k=1}A_{i,k}\times B_{k,j}$。
易得矩阵乘法满足结合率,那么如果我们要计算$A^k$,可以使用快速幂来加速。
矩阵在算法中一个很实用的地方在于矩阵加速。
一种是递推式加速,比如对于广义斐波那契数列 Luogu P1349 广义斐波那契数列:
$$
a_n=p\times a_{n-1}+q\times a_{n-2}
$$
我们可以构造这样的$2\times 2$矩阵:
$$
\begin{pmatrix}
0 & q \\
1 & p
\end{pmatrix}
$$
那么,求$a_n$就可以用矩阵加速解决:
$$
\begin{pmatrix}
a_1 & a_2
\end{pmatrix}
\times
\begin{pmatrix}
0 & q \\
1 & p
\end{pmatrix}^{n-2}
=\begin{pmatrix}
a_{n-1} & a_n
\end{pmatrix}
$$
另外一种运用是加速$DP$。Luogu P2106 Sam数
Sam 数具有以下特征:相邻两位的数字之差不超过 2。
考虑朴素的$DP$做法,此时我们的复杂度是$O(k)$,显然过不了。
但是注意到我们的$DP$维度是$k\times 10$,那么可以直接写出转移矩阵压掉$DP$的第二维,然后快速幂求解:
$$
\begin{array}{}
\begin{pmatrix}
dp_{1,0} & dp_{1,1} & dp_{1,2} & dp_{1,3} & dp_{1,4} & dp_{1,5} & dp_{1,6} & dp_{1,7} & dp_{1,8} & dp_{1,9}
\end{pmatrix} \\
\times
\begin{pmatrix}
1 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
1 & 1 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\
1 & 1 & 1 & 1 & 1 & 0 & 0 & 0 & 0 & 0 \\
0 & 1 & 1 & 1 & 1 & 1 & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & 1 & 1 & 1 & 1 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 & 1 & 1 & 1 & 1 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 & 1 & 0 \\
0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 & 1 \\
0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1
\end{pmatrix}^{n-1} \\ =
\begin{pmatrix}
dp_{n,0} & dp_{n,1} & dp_{n,2} & dp_{n,3} & dp_{n,4} & dp_{n,5} & dp_{n,6} & dp_{n,7} & dp_{n,8} & dp_{n,9}
\end{pmatrix}
\end{array}
$$
精妙。
数学部分小结
数学在信息学竞赛中真的很重要,越到后面要用到的数学知识越多。
NOIp之后要有计划的学习高中数学知识,看初等数论,寒假争取跟着高一一起学组合数学。
杂项
线段树
线段树精妙的在于其$Lazytag$,将区间添加的复杂度也优化至了$O(\log n)$级别。
这是一个基本的线段树:
struct node{
int l, r, data, add;
}t[400005];
void pushup(int p){
t[p].data = t[2*p].data + t[2*p+1].data;
}
void pushdown(int p){
if(t[p].add){
t[p*2].data += (t[p*2].r - t[p*2].l + 1) * t[p].add;
t[p*2+1].data += (t[p*2+1].r - t[p*2+1].l + 1) * t[p].add;
t[p*2].add += t[p].add;
t[p*2+1].add += t[p].add;
t[p].add = 0;
}
}
void build(int p, int l, int r){
t[p].l = l, t[p].r = r;
if(l == r){
t[p].data = a[l];
return;
}
int mid = (l + r) / 2;
build(2*p, l, mid);
build(2*p+1, mid+1, r);
pushup(p);
}
int query(int p, int l, int r){
if(t[p].l >= l && t[p].r <= r) return t[p].data;
pushdown(p);
int mid = (t[p].l + t[p].r) / 2;
int res = 0;
if(mid >= l) res += query(2*p, l, r);
if(mid < r) res += query(2*p+1, l, r);
return res;
}
void update(int p, int l, int r, int k){
if(t[p].l >= l && t[p].r <= r){
t[p].add += k;
t[p].data += k * (t[p].r - t[p].l + 1);
return;
}
pushdown(p);
int mid = (t[p].l + t[p].r) / 2;
if(mid >= l) update(2*p, l, r, k);
if(mid < r) update(2*p+1, l, r, k);
pushup(p);
}我线段树熟练度极低,打得很不熟练,离谱。
悬线法
悬线法用于解决极大子矩阵问题。
悬线的定义,就是一条竖线,这条竖线要满足上端点在整个矩形上边界或者是一个障碍点。然后以这条悬线进行左右移动,直到移至障碍点或者是矩阵边界,进而确定这条悬线所在的极大矩阵。
悬线法的转移非常简单:
l[i][j] = min(l[i][j], l[i-1][j]);
r[i][j] = max(r[i][j], r[i-1][j]);
up[i][j] = up[i-1][j] + 1;$l_{i,j}$,$r_{i,j}$,$up_{i,j}$表示$(i,j)$向左/向右/向上出发能够到达的最远距离。
Hash
$Hash$,哈希。其作用是把一个大数/字符串等等$hashable$,存储较为困难的元素,通过$hash$函数$f$映射到一个较小的数值上。
通常,对于一个大数,我们采用取模的方式构造$hash$函数,比如$f(x)=x\ mod \ p$,其中,$p$应该是一个大质数。
常见的大质数有:$10^9+7$,$998244353$等。
双Hash
当我们对一个大数取模时,尽管我们使用了一个大质数,但由于生日悖论,出现两个不同数被映射到同一个Hash值上的概率很大,此时我们采用双$Hash$的策略,这样出现重复$Hash$值的概率就会非常小。
字符串Hash
通常这样构造$Hash$函数:$f(s)=\sum_{k=0}^{len} s_i \times b^{len-k}$。
01分数规划
用于解决分数极值问题。
形式化的,01分数规划是要求一组$w_i \in \{0,1\}$,使得
$$
\frac{\sum_{i=1}^n a_i \times w_i}{\sum_{i=1}^n b_i \times w_i}
$$
取到极值。
01分数规划问题的通用解法是二分,考虑如何对式子进行化简:
$$
\begin{aligned}
& \frac{\sum_{i=1}^n a_i \times w_i}{\sum_{i=1}^n b_i \times w_i} > mid \\
\implies & \sum_{i=1}^n a_i w_i > mid \times \sum_{i=1}^n b_i w_i \\
\implies & \sum_{i=1}^n a_i w_i - mid \times \sum_{i=1}^n b_i w_i > 0 \\
\implies & \sum_{i=1}^n w_i \times (a_i - mid \times w_i) > 0
\end{aligned}
$$
那么重点就在于求$a_i - mid \times w_i$。
遇到01分数规划的题时,重点是分析题目,看针对当前题目,如何写二分的check()函数。
模拟退火
老消防员了
模拟退火($SA$,$Simulate \ Anneal$)。
为什么要使用模拟退火而不是爬山?
如果一道题的答案是一个单峰函数,那么,写爬山的确比模拟退火更加优秀,但事实上,更多时候,题目的答案都是一个多峰函数。
这个时候,如果我们使用爬山求解,很容易被一个小山峰骗走,从而找不到问题的最优解。
模拟退火算法是基于物理上退火现象的,在算法中体现为,设当前温度为$T$,当前解与当前最优解的差值为$\Delta E$,那么我们修改最优解的概率为:
$$
P(\Delta E)=\begin{cases}
1 & \Delta E \geq 0 \\
e^{\frac{-\Delta E}{T}} & \Delta E < 0
\end{cases}
$$
像这样以一定概率接受更劣解,使得我们更有可能找到一个问题的最优解。
模拟退火算法需要三个参数:初温$T_0$,降温系数$\Delta$,终止温度$T_k$。
算法写起来很容易,看一道简单题。Luogu P2210 Haywire
#include<bits/stdc++.h>
#define File(name) freopen(name".in", "r", stdin); freopen(name".out", "w", stdout);
#define Int inline int
#define Void inline void
#define Bool inline bool
#define DB inline double
#define LL inline long long
#define ri register int
#define re register
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef double db;
int n, ans, fd[15][5], pos[15];
LL read(){
ll n = 0; int f = 1; char ch = getchar();
while('0' > ch || ch > '9'){
if(ch == '-') f *= -1;
ch = getchar();
}
while('0' <= ch && ch <= '9'){
n = (n << 1) + (n << 3) + ch-'0';
ch = getchar();
}
return f * n;
}
Void write(ll x){
if(x/10) write(x/10);
putchar(x%10+'0');
}
Void input() {}
template<typename Type, typename... Types>
Void input(Type& arg, Types&... args){
arg = read();
input(args...);
}
Int randint(int l, int r){
return rand() % (r-l+1) + l;
}
int main(){
srand(time(0));
input(n);
for(ri i = 1; i <= n; i++) for(ri j = 0; j < 3; j++) input(fd[i][j]);
for(ri i = 1; i <= n; i++) pos[i] = i;
ans = 0x7fffffff;
for(ri times = 0; times < 300; times++){
for(register db T = 10000; T > 1e-12; T *= 0.99){
int x = randint(1, n), y = randint(1, n);
while(x == y) x = randint(1, n), y = randint(1, n);
swap(pos[x], pos[y]);
int totCost = 0;
for(ri i = 1; i <= n; i++) for(ri j = 0; j < 3; j++) totCost += abs(pos[i] - pos[fd[i][j]]);
totCost /= 2;
if(totCost < ans) ans = totCost;
else if(exp(ans-totCost) / T > (double)rand() / RAND_MAX) swap(pos[x], pos[y]);
}
}
write(ans);
return 0;
}还有一个卡时技巧:
while((double)clock() / CLOCKS_PER_SEC < 0.95) SA();此代码在题目所给的$Time \ Limit$内,不断跑模拟退火,找到最优解的概率更大。
注意不要把时限卡的太死,因为跑一次模拟退火还需要时间,卡时自然不会特别精确。
Ending
明天就是NOIp了,放平心态,打出自己的水准。
NOIp rp++
Liuxizai 2020.12.4
本作品采用 知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议 进行许可。
