Solution. LG6054 开门大吉 / 切糕模型
Description
$n$ 位选手参加比赛,共有 $m$ 套题,每套题包含 $p$ 个题目,第 $i$ 位选手答对第 $j$ 套题中第 $k$ 道的概率为 $f_{i,j,k}$。
每位选手选择一套题按顺序依次作答。若一位选手答对第 $i$ 题,会额外得到 $c_i$ 元奖励,注意每位选手只有答对了上一道题才会继续作答。
有 $y$ 条形如「第 $i$ 位选手的套题编号必须至少比第 $j$ 位的大 $k$」的限制。
给每一位选手分配一套题(不同选手可以相同),使所有人的期望奖励和最小,你需要求出这个最小值。
$1\le n,m,p\le 80,0\le y\le 10^3$
Solution
本题是经典的切糕模型,一般化的切糕模型如下:
有 $n$ 个整数变量 $x_i$,$x_i\in[1,m]$。$x_i$ 取 $j$ 的代价为 $a_{i,j}$。
有若干限制,每个限制形如 $x_u-x_v\le k$ 或 $x_u-x_v\ge k$。
给每个变量赋值,最小化总代价。
考虑使用最小割解决这类问题,基本的思想是,建出 $n$ 条长 $m+1$ 的链,$i\to i+1$ 的边权为当前变量取 $i$ 的代价,割掉这条边即表示让当前变量取 $i$,$S$ 向 $1$ 连流量为 $\inf$ 的边,$m+1$ 向 $T$ 连流量为 $\inf$ 的边。

流网络大概长这样,编号是随便标的。
接下来我们考虑限制如何描述。
如果 $x_u-x_v\ge k$,则对于每个 $i$,连 $(v,i)\to(u,i+k)$,流量为 $\inf$ 的边,这条边一定不会被断掉,这么做的意义是,如果 $(v,i)\to(v,i+1)$ 的边断掉,即 $x_v=i$,那么所有 $(u,j),j\le i+k$ 都应当被划入 $S$ 一侧的集合,所以链上被割的边应该在 $(u,i+k)$ 之后,即 $x_u\ge i+k$。

类似的,如果 $x_u-x_v\le k$,对于每个 $i$,连 $(u,i+k)\to(v,i)$ 的边即可。
当然,这样连边仍然存在问题,如下是一个例子。
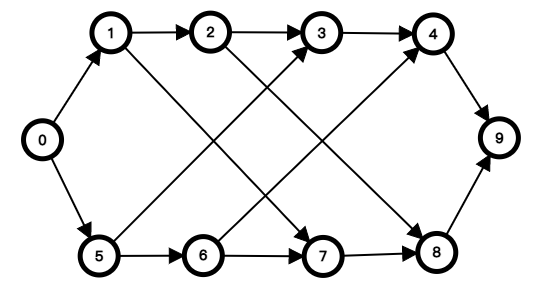
很显然,该网络对应的模型无解,但我们却可以通过割掉 $1\to2,3\to4,5\to6,7\to8$ 四条边求出一个显然不符合预期的解。
接下来,针对该问题我们有两种不同的解决方案。
-
在连接 $5\to3,6\to4$ 时,由于 $7,8$ 没有点可连,我们就将他们放弃了,但问题也出在这里,假如错误的将 $7$ 划入 $S$,而 $6$ 划入 $T$,$7$ 的限制就无法表达,所以我们可以连接 $7\to4,8\to4$ 确保所有限制都被准确描述。
另一种理解方式是,这样确保了在任何无解的时候都存在从 $S\to T$,流量为 $\inf$ 的路径。
-
出现问题的原因是我们在一条链上割了多于 1 条边,从而导致链上每个点被划分到的集合变的混乱,这种情况不应该出现。
我们可以考虑连接 $(u,i+1)\to(u,i)$,流量为 $\inf$ 的反向边,这样确保了如果 $(u,i)$ 被划分到 $S$,所有 $(u,j),j<i$ 都被划分到 $S$,这样一条链上的点一定是前一部分属于 $S$,后一部分属于 $T$,从而也保证了只会割一条边。
同样的,我们也可以理解成构造了一条 $S\to T$,流量为 $\inf$ 的路径。
具体的,回到本题,我们可以方便的计算出第 $i$ 位选手做第 $j$ 套题的期望得分为:
$$
\sum_{k=1}^pc_k\prod_{t=1}^kf_{i,j,t}
$$
然后按照上述模型建图求解即可。
Code
namespace Main{
const int N = 10005;
const int M = 1000005;
const double inf = 1e10;
const double eps = 1e-6;
int t, n, m, p, y, S, T, c[N];
int cnt, d[N], start[N];
double val[M], a[100][100];
bool vis[N];
struct edge{
int to, id;
edge() {}
edge(int to, int id): to(to), id(id) {}
};
vector<edge> g[N];
void add(int u, int v, double w){
// cerr << u << ' ' << v << ' ' << w << endl;
cnt++;
assert(cnt <= 500000);
g[u].emplace_back(v, cnt<<1);
g[v].emplace_back(u, cnt<<1|1);
val[cnt<<1] = w;
val[cnt<<1|1] = 0;
}
bool bfs(int s, int t){
queue<int> q;
memset(d, -1, sizeof(d));
q.push(s);
d[s] = 0;
while(!q.empty()){
int u = q.front(); q.pop();
start[u] = 0;
for(edge v: g[u]){
if(val[v.id] > eps && d[v.to] == -1){
d[v.to] = d[u] + 1;
q.push(v.to);
}
}
}
return d[t] != -1;
}
double dfs(int u, double in){
if(u == T) return in;
double out = 0;
for(int i = start[u]; i < g[u].size() && in - out > eps; i++){
edge v = g[u][i];
start[u] = i;
if(val[v.id] > eps && d[v.to] == d[u] + 1){
double res = dfs(v.to, min(val[v.id], in - out));
if(res < eps) d[v.to] = -1;
val[v.id] -= res;
val[v.id^1] += res;
out += res;
}
}
return out;
}
double dinic(int s, int t){
double res = 0;
while(bfs(s, t)) res += dfs(s, inf);
return res;
}
void Main(){
input(t);
while(t--){
for(int i = 0; i <= T; i++) g[i].clear();
cnt = 0;
input(n, m, p, y);
for(int i = 0; i < p; i++){
input(c[i]);
if(i) c[i] += c[i-1];
}
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
a[j][i] = 0;
double mul = 1, tmp;
for(int k = 0; k < p; k++){
scanf("%lf", &tmp);
if(k) a[j][i] += mul * (1 - tmp) * c[k-1];
mul *= tmp;
}
a[j][i] += mul * c[p-1];
}
}
auto id = [=](int x, int y){
assert(x >= 0 && y >= 0 && x * (m + 1) + y < N);
return x * (m + 1) + y;
};
S = n * (m + 1), T = S + 1;
for(int i = 0; i < n; i++){
add(S, id(i, 0), inf); add(id(i, m), T, inf);
for(int j = 0; j < m; j++){
add(id(i, j), id(i, j + 1), a[i][j]);
add(id(i, j + 1), id(i, j), inf);
}
}
for(int i = 0; i < y; i++){
int u, v, w;
input(u, v, w); v--, u--;
for(int j = max(0, -w); j <= m && j + w <= m; j++) add(id(v, j), id(u, j + w), inf);
}
double ans = dinic(S, T);
if(inf - ans > eps) printf("%.6lf", ans), puts("");
else puts("-1");
}
return;
}
} // namespace本作品采用 知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议 进行许可。
