做题笔记 since 2022.4.4

LG4314 CPU监控

线段树维护历史最值的模版题，要求支持区间加和区间推平，查询区间最大值以及区间历史最大值。

首先容易想到维护区间最大值 max，区间历史最大值 hmax，区间加的 tag add 以及区间推平的 tag cov。

这里存在的细节就是，在一次推平操作后，之前的 add 一律失效，并且在有推平操作的情况下，接下来的 add 就都可以被转换为推平操作了，只需要对应的修改 cov 即可，这样在实现时会方便许多。

然后你会发现这还不够。

比如说区间加 $10$，然后区间加 $-5$，这个时候下传标记，我们就会用 $5$ 来更新儿子的 hmax，而这显然是错误的，所以我们另外需要维护一个历史最大的 add，以及对应的历史最大的 cov，这也是另一个我们把 add 转换为 cov 的原因，就是为了避免两个历史最大标记的冲突。

标记下传的过程一定要仔细实现，要不然很容易漏掉某个标记的更新。

LG3736 字符合并

区间 dp（注意到 $n\le300$），状压 dp（注意到 $k\le 8$）。

长度为 $len$ 的串经过若干次变换后，长度最终会变为 $(len-1)\bmod(k-1)+1$。

那么转移方程显然：
$$
f_{l,r,S\times2+0/1}=\max\{f_{l,p,S}+f_{p+1,r,0/1}\}
$$

这里我们要求 $r-p-1\equiv 0\pmod{k-1}$，也就是要求 $[p+1,r]$ 变换之后长度应为 $1$。

另外在 $r-l\equiv0\pmod{k-1}$ 时要特殊处理，先让 $[l,p]$ 和 $[p+1,r]$ 合并出长度为 $k$ 的串 ，然后再整体合并一次，加上贡献即可。

总复杂度 $O\left(\dfrac{n^32^k}{k}\right)$，但是上界很松，可以通过。

CF452F Permutation / LG2757 等差子序列

询问给定 $1\sim n$ 的排列中是否存在一个长度为 $3$ 的等差子序列。

从左到右扫一遍，记录每个数是否出现过，考虑某个时刻，现在我们拿到的数是 $a_i$，假如存在以 $a_i$ 为中项的等差子序列，则意味着存在 $a_i-k$ 和 $a_i+k$，一个在之前出现过，一个没出现过。

换言之，假设不存在以 $a_i$ 为中项的等差子序列，任取 $a_i-k$ 和 $a_i+k$，它们的出现状态应该相同，也就是说整个状态串构成了以 $a_i$ 为中心的回文串，用线段树维护 hash 即可快速判断。

LG2542 航线规划

无向图上动态删边，询问两点间割边数量，保证图中无自环、重边，保证图始终连通。

删边不好维护，考虑将操作离线下来逆序处理，删边变为加边。

tarjan 求割边肯定不现实，考虑另外一种做法，先把 dfs 树求出来，对于任意一条非树边 $u\to v$，在 dfs 树上将 $u\rightsquigarrow v$ 路径上所有边打上标记，那么这些边不可能是割边，反之所有没有被标记的边一定是割边。

于是我们现在只需要支持树上的路径覆盖和路径求和两种操作，树剖维护即可。

LG5310 Ynoi2011 遥远的过去

为什么会无聊到来做 Ynoi 呢

其实是从 等差子序列 那题过来的，一个是线段树维护 hash，一个是平衡树，感觉很 nb。

感觉我学编程的经历和题目背景有异曲同工之妙。

区别大概在于，我参加了一次科创大赛，然后做了个感觉很 nb 的游戏，代码也非常炫酷，这玩意现在在旧电脑的硬盘里还找得到，结果没拿奖，从此对这种科创大赛彻底丧失了兴趣，觉得这种东西水太深。

机缘巧合跑去 hsy 学信竞，当时在教 C++，但是我已经学过 Python 了，就觉得 C++ 跟 Python 比起来实在是显得十分丑陋，然后参加选拔考试（笔试）的时候，因为代码写的比较不合常规，被扣了好多分，那个时候觉得 OI 说是竞赛还是脱不开应试教育的恶劣风气，但还是学下来了，就成了现在这个样子，越来越菜了 /fad。

但是这里是做题笔记，而不是给我写奇怪文字的地方，所以我们回到题目上来。

类似于字符串匹配，只不过我们只需要两个串的 rank 数组相同即可。

kmp 看着不太合理，所以考虑 hash。

文本串始终不变，那我们大可直接把文本串所有长度为 $m$ 的子串的 hash 值算出来，丢到一个 map 里去。然后用平衡树动态维护模式串的 hash 值，直接在 map 里查询即可。

关于 hash 函数的选取上，大体上有两种思路，$\sum rank_i\times base^{i}$ 以及 $\sum i\times base^{rank_i}$，为了方便快速求出文本串所有长度为 $m$ 子串的 hash 值，这里采用前者（现在想想用后面一个实现起来也不困难）。

平衡树动态维护 hash 值的时候，我们考虑如何将两个串 $L,R$ 合并在一起，由于是在平衡树上，$L$ 的 rank 肯定整体比 $R$ 小。

在合并的时候，我们相当于将 $R$ 的 rank 整体提高了 $len(L)$，反映在 hash 值上，就是加上了 $\sum len(L)\times base^{rank_i}$，所以，我们再额外维护一个 $\sum base^{rank_i}$ 即可。

单模数试了半天过不去，实在没办法就魔改了一个双模数。

复杂度 $O(n\log n)$。

PJ21618 ExPR#1 乘积 / ABC239Ex Dice Product 2

感觉 public judge 的题解一直都写的非常简洁，尤其是对于 A 题，大概是搬题人水平普遍太高，认为这种题完全是签到题不需要多讲，但是对于我这种人确实是不太友好。

讲一讲我的一些想法。请注意如无特殊说明，变量的取值均为整数。

首先我们希望设 $f_i$ 表示当 $M=i$ 时，或 $M>i$ 时的期望步数，后者似乎并不方便转移，而前者的问题也很明显，我们不知道 $f_i$ 会由哪些状态转移而来，概率的计算上也就变得更加复杂了，同时还存在的问题是终止状态并不唯一，不方便统计答案。

所以我们考虑这样的一步转化，将 dp 的过程倒过来，也就是乘法变为除法，初始时我们让 $f_i(i>m)=0$，也就对应了初始状态，由于对于任一状态而言，能够转移到的状态都恰好有 $n$ 个，我们容易得到转移方程：
$$
f_i=1+\frac{1}{n}\sum_{j=1}^n f_{ij}
$$
方程右边出现了 $f_i$，我们将其挪到左边来，容易得到：
$$
f_i=\frac{n}{n-1}+\frac{1}{n-1}\sum_{j=2}^nf_{ij}
$$
暴力转移即可，最终答案即为 $f_1$（对应正序转移时的起始状态），至此我们得到了一个 $O(nm)$ 的算法。

pjudge 的题解中没有提到上述对于问题的转化 /yun。

接下来，我们观察可以发现，对于 $\left\lfloor \dfrac{m}{i} \right\rfloor$ 相同的 $i$，$f$ 值一样。

这一点可以用归纳法证明，对 $i$ 进行归纳，$f_i$ 会从 $f_{ij},j\in[2,n]$ 转移而来，考虑若 $\left\lfloor\dfrac mi\right\rfloor$ 相同，则 $\left\lfloor\dfrac m{ij}\right\rfloor=\left\lfloor\dfrac{\left\lfloor m/i\right\rfloor}{j}\right\rfloor$ 相同，于是易证。

但是，如果我们要深究存在这一现象的原因，考虑这样一件事情。

对于 $f_i$ 和 $f_j$，我们设 $x$ 表示使 $ix>m$ 最小的 $x$，类似的，对于 $j$ 设 $y$，假如 $f_i$ 和 $f_j$ 相等，则 $x$ 和 $y$ 应该是相等的，这一点从感性上来说应该容易理解。于是我们可以得到 $\left\lceil\dfrac{m+1}{i}\right\rceil=\left\lceil\dfrac{m+1}{j}\right\rceil$，我们知道 $\left\lceil\dfrac{m+1}{i}\right\rceil=\left\lfloor\dfrac{m}{i}\right\rfloor+1$，所以原命题同样得证。

所以，我们设 $g_i$ 表示 $f_k,\left\lfloor\dfrac{m}{k}\right\rfloor=i$ 的值，有：
$$
g_i=1+\frac1n\sum_{j=1}^ng_{\lfloor\frac{i}{j}\rfloor}
$$
化为：
$$
g_i=\frac{n}{n-1}+\frac{1}{n-1}\sum_{j=2}^ng_{\lfloor\frac{i}{j}\rfloor}
$$
记搜即可。

根据整除分块的分析方法，我们知道总状态数为 $|\{\lfloor m/k\rfloor\}|=\sqrt m$，总复杂度为 $O\left(\sum\limits_{i=1}^\sqrt{m}\sqrt{m/i}\right)$。

不会算，所以积一下：
$$
\begin{aligned}
&\int_{1}^{\sqrt m}\sqrt{\frac{m}{x}}\mathrm{d} x\\
=&\int_{1}^{\sqrt m}\sqrt m\cdot x^{-\frac12}\mathrm dx\\
=&O(m^{\frac34})
\end{aligned}
$$
实际上和杜教筛是一样的。

LG5514 柠檬

考虑每一段的端点颜色一定相同，要不然多余的部分也无法对当前段作贡献。

然后分颜色进行斜率优化即可。

值得注意的是在本题中，我们希望最大化 dp 的值，所以要维护的是上凸包，同时 $x$ 单调增，$k$ 单调增，那么就应当使用单调栈。

是道斜率优化好题。

LG6400 UMNOZAK / BZ1183 Umnozak

首先是显然的数位 dp，但是题目所定义的「自积」并不方便直接维护。

对于 $x=\overline{a_1a_2\dots a_k}$，定义 $p(x)=\prod_i a_i$，因为 $a_i\in[0,9]\cap \mathbb{Z}$，所以 $p(x)$ 的质因子仅有 $2,3,5,7$。

我们有 $p(x)\le 9^k$，$x=\sum_i a_i10^i>10^k$，于是 $x>p(x)$。

又因为 $A,B\le10^{18}$，于是 $p(x)<10^9$。

我们知道，$10^9$ 以内质因子仅有 $2,3,5,7$ 的数极少，事实上，如果你枚举一下容易发现这样的数仅有 $5194$ 个。

那么考虑枚举满足条件的 $p(x)$，然后进行数位 dp，记录当前各位数字之积中 $2,3,5,7$ 质因子的个数，这里略去实现细节。

总复杂度为 $O(k\log^5B)$，其中 $k=5194$，这个 5log 实际上是 $2,3,5,7,10$ 为底数各一个，我也不知道这个复杂度分析是不是对的，从实际效率来说应该没什么问题。

BZ3329 Xorequ

给出的方程是：
$$
x\oplus3x=2x
$$
两边同时异或 $x$：
$$
\begin{aligned}
3x&=x\oplus 2x\\
x+2x&=x\oplus 2x
\end{aligned}
$$
我们知道 $x+2x=x\operatorname{|}2x+x\operatorname{\&}2x$，$x\oplus 2x=x\operatorname{|}2x-x\operatorname{\&}2x$，由于这两者相等，于是：
$$
x\operatorname{\&}2x=0
$$
也就是说，$x$ 中不存在相邻的两个 $0$。

对于第一问直接数位 dp 即可，第二问考虑设 $f_{i,0/1}$ 表示考虑前 $i$ 位，以 $0/1$ 结尾的方案数，有转移：
$$
\begin{cases}
f_{i,0}=f_{i-1,0}+f_{i-1,1}\\
f_{i,1}=f_{i-1,0}
\end{cases}
$$
实际上和 fibonacci 数列一致，本来想用通项公式直接水，但是似乎 $\sqrt5$ 在 $\bmod 10^9+7$ 下不存在二次剩余，所以老老实实矩阵加速即可。

LG6669 清华集训2016 组合数问题

考虑 lucas 定理：
$$
\binom nm \equiv \binom{\lfloor n/p\rfloor}{\lfloor m/p\rfloor}\binom{n\bmod p}{m\bmod p}\pmod p
$$
实际上就是对 $n$ 和 $m$ 进行了 $p$ 进制拆分，然后每一位取组合数再全部乘起来。

在本题中也一样，如果将 $i,j$ 进行 $k$ 进制拆分后分别为 $\overline{a_1a_2\dots a_l}$ 和 $\overline{b_1b_2\dots b_l}$，那么有：
$$
\binom{i}{j}\equiv\prod_{t=1}^l\binom{a_t}{b_t}\pmod k
$$
由于保证了 $k$ 为质数，$\dbinom{a_t}{b_t}=0$ 当且仅当 $a_t<b_t$，所以题目要求等价于 $i$ 的 $k$ 进制表示中至少有一位比 $j$ 的小。

容斥一下变为每一位都不小于 $j$ 后数位 dp 即可。

PJ21613 PR#1 删数

其实很简单，但是之前看题解就是没有 get 到点。

首先题意的转化是容易理解的，求出差分数组，然后操作变为合并两个相同的数变为原来的两倍。

从二进制来看，变为原来的两倍意味着左移，而左移显然不会对 $d_i/\mathrm{lowbit}(d_i)$ 进行改变，换言之也就意味着 $d_i/\mathrm{lowbit}(d_i)$ 不同的两个数永远不可能被合并。

这意味着我们可以按照 $d_i/\mathrm{lowbit}(i)$ 对原序列进行分段，在每一段中我们可以将每个数都只保留 $\mathrm{lowbit}(d_i)$，这也就完成了「不妨设 $d_i$ 均为 $2$ 的幂次」这一步。

设 $f_i$ 表示前 $i$ 个数至少能合并为多少段，$g_{i,j}$ 表示在每一段中，以 $i$ 为右端点合并出 $2^j$ 时的左端点，递推转移即可，复杂度为 $O(n\log V)$，其中 $V$ 为值域。

或者说我们也可以不分段，直接设 $g_{i,j}$ 表示以 $i$ 为右端点合并出 $j$ 时的左端点，当然要求 $j=d_i\times2^k$，用 map 维护状态即可，代码实现更为简单粗暴，复杂度由于 map 变为 $O(n\log^2 V)$，但也足以通过此题。

PJ21614 PR#1 守卫

每个连通块可以只保留最小生成树，因为每个守卫负责的连通块最终肯定是只会保留最小生成树的，我们任取原图的一个导出子图，导出子图也一定存在一个最小生成树是原图最小生成树的子图。

剩下的部分容易用网络流描述。

• 守卫向可以前往的结点连费用为 0，流量为 1 的边。
• 生成树上的边向两个端点连费用为边权，流量为 1 的边。
• 源点向守卫和边连费用为 0，流量为 1 的边。
• 原图中结点向汇点连费用为 0，流量为 1 的边。

然后判合法一方面需要所有守卫被匹配，一方面需要所有原图中结点被匹配。

你可以选择先只连守卫 $\to$ 结点的边，跑一次费用流判断前者，再把树边 $\to$ 端点的边连上，再跑一次费用流判断后者，第一次流的流量是不用撤回的。

PJ21625 PR#3 最小生成树

给一种与题解不同的，更容易理解的，但是很可能存在错误的证明。

我们的网格图从上到下行数递增，从左到右列数递增。

Lemma. 1 最上面一行的所有横向边和最左边一列的所有纵向边一定会被选取。

也就是像这样：

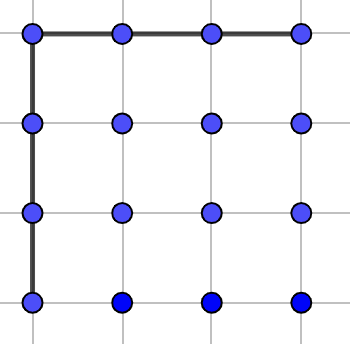
Proof. 我们考虑任意的一个生成树：

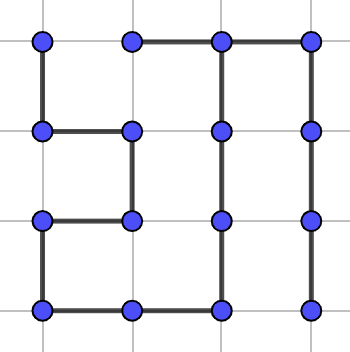
第二行缺纵向边，第一列缺横向边，我们希望通过从同一行或同一列调整一条边的位置，来使得生成树符合条件。

由于保证了 $A,B,C,D$ 单调不降，所以这样调整必然不劣，接下来只需要证明一定存在合法的调整方案。

在断开一条边之后，整棵树会被分为两个连通块，为了使修改后的图仍然是生成树，我们需要保证接下来所连边的两个端点分别属于这两个连通块。

那么我们不妨考虑这样一个过程：首先连上缺失的横向边/纵向边，此时图中必然会出现一个环，我们只要删去环上另外一条与缺失边处于同一列/行的边即可，这样的边一定存在，原理与勘根定理类似。$\blacksquare$

在这个例子中，修改后的图如下：

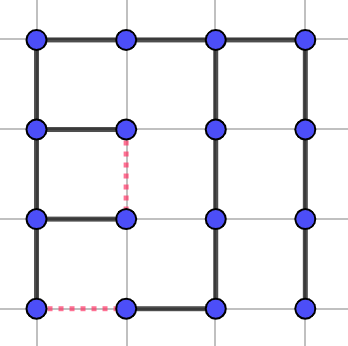
删去的边用粉色虚线代替，下同。

Lemma. 2 在 Lemma. 1 的基础上，必然存在一个最优解，使得 $\forall (x,y),x\in[2,n],y\in[2,m]$，使得边 $(x,y)\to (x-1,y)$ 和 $(x,y)\to(x,y-1)$ 中「恰好」存在一条。

换言之，就是在固定最上面一行的横向边和最左边一列的纵向边后，余下未连边的结点都「恰好」向左或向上连了一条边。

Proof. 首先，显然任意这样连边都是合法的，可以归纳证明连通性，接下来由总边数可知图中不存在环，故必然是一棵生成树。

我们仍然考虑将任意生成树调整至符合条件，这里接着使用 Lemma. 1 中的例子。

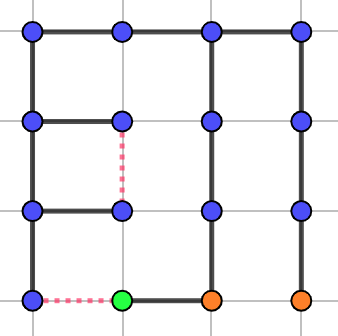
此时图中会存在若干个点既没有向左连边，也没有像上连边。在例子中，这样的点被标记为了绿色，我们称这种点为「空」的，而与之相反的，我们称既向左连边又向上连边的点为「满」的。

对于一个空点，在其右下方必然存在一个满电。

否则，考虑满点与其所有左上方点构成的导出子图，这个子图将包含 $|V|$ 条边，于是必然存在一个环，这与原图是生成树矛盾。

于是，我们可以任取满点对应的横向边或纵向边，移动到空点上即可，由于满点在空点的右下方，这样调整必然不劣。$\blacksquare$

在这个例子中，调整后的图如下：

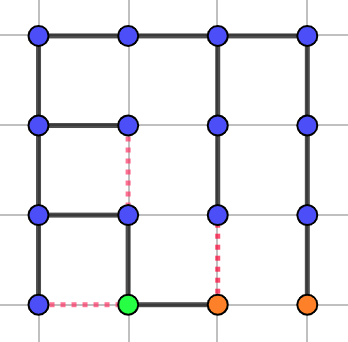
根据 Lemma. 1 和 Lemma. 2，我们容易得到一个构造答案的方式，首先固定最上面的横向边与最左边的纵向边，然后对于余下所有点，贪心的选择向左连边或向上连边即可。

注意到 $\min\{A+B,C+D\}=A+B+[A-C+B-D>0](A-C+B-D)$，于是容易通过二分+前缀和优化复杂度至 $O(n\log m)$。

本作品采用 知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议 进行许可。