做题笔记 2024 NFLS NOI 模拟赛

2024.5.21 展开目录

树数术展开目录

给一颗 $n$ 个点的树和一个长为 $m$ 的序列 $a_{1 \dots m}$ ，序列中每个数表示树上的一个节点。 $q$ 次询问，每次询问给出 $a$ 的 $k$ 个子区间，将这 $k$ 个子区间顺次拼接成新的序列，求新序列上有多少个数是前缀 $lca$ 。

假设 $n, m, \sum k$ 同阶。查多个区间的拼接和查一个区间没什么本质区别。

前缀信息可以用兔队线段树维护。使用 $O (n \log n) - O (1)$ 的 $lca$ 容易将总复杂度做到 $O (n \log^{2} n)$ 。这里注意兔队线段树可以在线段树结点上只维护右儿子的信息，这样不需要信息的可减性，但是如果维护整个结点的信息可以在查询时增加一些剪枝，从而优化一定的常数。本题只维护右儿子信息应该会被卡常。

查询前缀信息在不强制在线时可以离线之后用扫描线 + 二分解决。本题用这种方式容易做到 $O (n \log n)$ 。

Perotation 展开目录

给一个 $1 \sim n$ 的排列 $a$ 。定义一次操作为选取连续的三个数 $a_{i - 1}, a_{i}, a_{i + 1}$ ，要求 $a_{i - 1} < a_{i} < a_{i + 1}$ ，然后将他们分别修改为 $a_{i + 1}, a_{i - 1}, a_{i}$ 。 $q$ 次修改，每次修改交换 $a_{x}, a_{y}$ ，然后求最长的 $a$ 的后缀满足其能够从一个单调递增的序列通过若干次操作得到。

一个序列是满足条件的当且仅当每个数后面比他小的数的个数均为偶数。于是我们试图维护 $r_{i}$ 表示 $a_{i}$ 后面比 $a_{i}$ 小的数的个数的奇偶性，询问相当于查序列上最后一个 $1$ 的位置。

考虑分块。不妨设 $a_{x} < a_{y}$ ，则一次修改会对满足 $x < i < y, a_{x} < a_{i} < a_{y}$ 的 $r_{i}$ 进行翻转， $x, y$ 处的值可以暴力重新计算，这个形式可以块内用线段树维护做到 $O (n \sqrt{n} \log n)$ ，亦可以直接用 bitset 维护二维偏序做到 $O (n^{2} / w + n \sqrt{n})$ ，根号来自维护表示值 $[1, i]$ 所在位置的 bitset。

一个重要的观察是，本题在询问时我们只关心一个块内是否存在 $1$ ，于是我们可以只维护 $r_{i}$ 的差分数组，这并不影响 $1$ 的存在性。考虑将 $r_{i}$ 按照 $a_{i}$ 从小到大的顺序排序，这样每次整块的修改就变成了区间翻转，转差分后即为单点修改，这就是容易维护的了。这里需要使用 std::lower_bound，会多一个 $\log$ ，但是 std::lower_bound 常数很小，没必要将其替换掉。总复杂度视为 $O (n \sqrt{n})$ 。

术数树展开目录

定义 $k$ 进制异或为 $k$ 进制不进位加法。

给一张无向图，边有边权。一条路径的权值为路径上所有边的边权的 $k$ 进制异或和。求 $u ⇝ v$ 的路径的最小权值（一条边可以经过任意多次）。

$k = 2$ 时这个问题是经典的，取任意 dfs 树然后将所有返祖边构成的环的权值丢到线性基里即可。

$k$ 为其他值时做法完全相同。我们可以对任意 $k \geq 2$ 构建 $k$ 进制下的异或线性基，具体方式查看这篇博客。

2024.5.24 展开目录

棋盘展开目录

有一个 $n \times m$ 的棋盘，初始时有一个棋子放在 $(1, 1)$ 上。Alice 和 Bob 轮流操作，Alice 先手，每人每次可以将棋子移到同行或同列的某个格子上，也可以立刻终止游戏。每个格子被移到的次数需要严格小于 $10^{9}$ 。给两个长度分别为 $n, m$ 的序列 $a, b$ ，格子 $(x, y)$ 的权值为 $a_{x} + b_{y}$ ，Alice 希望最终棋子所在的格子的权值尽可能小，Bob 希望权值尽可能大。求最终棋子所在格子的权值。

Alice 希望权值尽可能小，Bob 希望权值尽可能大，在这样的目标下，我们可以首先二分答案 $m i d$ ，此时 Alice 希望权值 $\leq m i d$ ，我们检查 Alice 是否能够获胜即可。这样做的好处是，所有格子被简单的分成了两类，一类 Alice 希望到达，另一类 Bob 希望到达。

感性理解，限制格子被移到的次数小于 $10^{9}$ 和限制每个格子只能经过一次是等价的，可以考虑如果必败方让棋子走了回头路，必胜方可以反着再走回来，最后必败方必须选择一个别的点前往。虽然这个证明一点道理都没有。

我们称权值 $\leq m i d$ 的点为白点，权值 $> m i d$ 的点为黑点。

另外需要注意到本题中双方都可以在轮到自己操作时选择结束游戏，所以如果 $(1, 1)$ 为白点，Alice 立刻获胜，此外 Alice 只能将棋子移至黑点，Bob 只能将棋子移至白点，否则对方都会立刻获胜。有效的移动只发生在异色点之间，这样就构建出了本题的二分图博弈模型。

二分图博弈的结论是，先手必胜当且仅当起点被包含在二分图的所有最大匹配中，证明并不困难。

于是就有了一个暴力的做法，建出 $O (n^{2})$ 个点 $O (n^{3})$ 条边的二分图然后跑最大匹配，判断起点是否一定被最大匹配包含可以直接将起点删掉再跑一遍，单次检查复杂度为 $O (n^{4})$ 。

考虑直接在原来的网格图上做最大匹配，不过匹配这个形式并不方便描述，可以将其转化为最大独立集。一个点向同行同列的异色点连边，所以最大独立集相当于选取一些行和列，选取同时落在这些行和列内的白点，以及同时落在其余行和列内的黑点，最大化所选点的个数。

如果我们将 $a, b$ 从小到大排序，则白点和黑点的分界线是一个从右上到左下的阶梯形，左上方是白点，右下方是黑点。容易发现最优情况下我们总是选择所有行和所有列的一个前缀。于是我们枚举行的分界线，最优的列分界线随行分界线的下移而右移，做一个双指针即可。删掉起点对这个过程的影响不大，特殊处理起点即可。单次检查复杂度为 $O (n)$ ，总复杂度 $O (n \log V)$ 。

2024.5.25 展开目录

树的镜像 / LG4672 [BalticOI 2011 Day2] Tree Mirroring 展开目录

做法很多，关键在于定位到一个叶子或者一组对应点。

叶子总是二度点，但二度点未必是叶子。我们考虑广义串并联图方法，不断缩二度点。特判掉链和环的情况，不难发现，若图合法，则我们总是能缩出重边，那么一个叶子就是其中一条边对应的原图上路径的中点。更简便的方法是，若 $u, v$ 间缩出了重边，则 $u, v$ 一定是对应点。

据此我们就可以定位出所有的叶子。分别以 $u, v$ 为起点 bfs，一个点为叶子当且仅当其到 $u$ 的距离与到 $v$ 的距离相同。

我们可以用所有叶子将图分成两部分，用树哈希判断以 $u, v$ 为根的树是否同构即可。注意本题中叶子是需要相互区分的，解决方法是给每个叶子随机分配权值。

注意细节的处理。

2024.5.27 展开目录

排序幻觉展开目录

给一个长度为 $n$ 的序列 $a$ ，支持单点修改，每次修改后查询最小的 $x$ 使得 $\forall i \in [1, n) a_{i} \oplus x \leq a_{i + 1} \oplus x$ 。

小于等于这个限制实际上是非常强的，这个条件满足当且仅当两数相同，或在两数最高的不同的二进制位上，较小数为 $0$ ，较大数为 $1$ 。所以如果要求 $a_{i} \oplus x \leq a_{i + 1} \oplus x$ ，我们找到 $a_{i}$ 和 $a_{i + 1}$ 最高的不同的二进制位，视两数在该位上的取值会限制 $x$ 在该位上必须取 $0$ 或 $1$ 。我们用桶维护所有相邻两数对每个二进制位的限制情况，单点修改时只会影响两对相邻数，暴力更新信息即可。总复杂度 $O ((n + q) \log V)$ 。

图展开目录

给一张 $n$ 个点的无向图，求它的连通导出子图的个数。答案对 $2$ 取模。

保证无向图中的每条边 $(u, v)$ 满足 $| u - v | \leq 12$ 。

由于有 $| u - v | \leq 12$ 我们考虑 dp，从小到大逐个加点，这样我们只需要维护有关最后 $12$ 个点的信息。但是这样仍然很难做，由于要求得到的导出子图连通，我们必须维护最后 $12$ 个点的连通性信息，这样可以得到一个 $O (Bell (d) poly (n))$ 的做法，其中 $d = 12$ 。

我们需要利用答案对 $2$ 取模这一性质，使得合法的导出子图贡献为 $1$ ，不合法的导出子图贡献为 $0$ 。考虑一个导出子图合法当且仅当其恰好有一个连通块，若另一个导出子图的贡献为 $2^{c - 1}$ ，其中 $c$ 为连通块个数，则对 $2$ 取模后就达到了我们想要的效果。

为了让式子更好看一点，我们将贡献改为 $2^{c}$ ，并让答案对 $4$ 取模，这样不合法的导出子图贡献仍为 $0$ 。考虑为 $2^{c}$ 赋予组合意义，这可以视作为所有点黑白染色，要求相同连通块内点同色的方案数。

这样就可以 dp 了。设 $f_{i, S, T}$ 表示前 $i$ 个点，最后 $12$ 个点中选了 $S$ ，其中黑点为 $T$ ， $T \subseteq S$ 。

复杂度 $O (n 3^{d})$ 。

分身术展开目录

从 $n$ 个区间中选出尽可能多的区间使得这些区间能被分成 $k$ 组，每组内的区间两两不交。

对每个 $1 \leq k \leq m$ 求答案。

$k = 1$ 时的贪心是经典的，将区间按 $r$ 排序，依次考虑每个区间能选则选即可。

事实上 $k$ 更大时也是类似的，可以说明，选出的区间合法当且仅当不存在某个位置被 $> k$ 个区间覆盖。证明考虑 Dilworth 定理，将能分成 $k$ 组这一「最小链覆盖」转换为「最长反链」即可。

这样容易做到 $O (n m \log n)$ 。瓶颈在于要对每个 $k$ 求答案。

另一个符合直觉的事实是若一个区间在 $k = k_{0}$ 时被选，则 $k = k_{0} + 1$ 时它也会被选。

这样若我们已经有了 $k = k_{0}$ 时的答案，想要求 $k = k_{0} + 1$ 的答案只需要在原答案上添加区间即可。此时我们不能暴力将所有区间扫一遍，用线段树二分支持快速找到下一个可选的区间即可。总复杂度 $O ((n + m) \log n)$ 。

2024.5.28 展开目录

语言学展开目录

给 $n$ 个文本串 $S_{1}, \dots, S_{n}$ 以及 $m$ 个模式串 $T_{1}, \dots, T_{m}$ 。对于所有有序对 $(i, j, k)$ ，若存在 $S_{i}$ 的非空后缀及 $S_{j}$ 的非空前缀的拼接等于 $T_{k}$ ，则产生 $w_{k}$ 的贡献。求所有有序对的贡献和。

我们容易求解的是这样的问题：每有一个 $S_{i}$ 的非空后缀和 $S_{j}$ 的非空前缀的拼接等于 $T_{k}$ ，就对答案产生 $w_{k}$ 的贡献。换言之，一个模式串可以在一对字符串的拼接中被统计多次。此时只需要对所有模式串正反分别建 AC 自动机即可。

现在问题是如何去重。

若一个模式串 $T$ 在一个拼接中多次出现，则它们的间隔一定是 $T$ 的周期。并且我们发现，大多数时候，这个间隔总是 $T$ 的最小周期。更具体的，若模式串出现了 $\geq 3$ 次，它们的出现位置一定是公差为最小周期的等差数列（此处证明的核心在于所有 occurence 的交集非空）。对于这些间隔为最小周期的重复统计，容易发现我们只需要从答案中减去 $period (T) + T$ 的贡献即可，这里 $period (T)$ 指 $T$ 的最小周期。

现在只需要考虑间隔不是最小周期倍数的情况，根据 border 理论，所有周期可以被划分成 $\log$ 个等差数列。此处我们考虑和最小周期不在同一等差数列中的周期即可。由于周期与 $T$ 的拼接最多只在文本串的拼接中出现一次，不需要考虑算重的问题。于是可以对每段等差数列快速计算答案，单次复杂度关于等差序列首项对应的 border 长度线性。border 划分成等差数列时，一个等差数列的首项大于上上一个等差数列末尾的两倍，所以所有首项的长度总和是 $O (| T |)$ 的。

注意这部分统计中有可能重复统计最小周期的倍数，最后要将这部分贡献去掉。一个例子是 $aabaaabaa$ ，最小周期为 $aaba$ ，在取到其倍数 $aabaaaba$ 之前还有周期 $aabaaab$ ，于是倍数落到了后面的等差数列里。

总复杂度为 $O (| S | | Σ | + | T |)$ 。

航行展开目录

有 $n$ 个点排成一排，同时给定长度为 $n$ 的实数序列 $p$ ， $p_{i} \in [0, 1]$ 。有一个人在点之间按如下方式随机游走：若这个人当前位于点 $x$ ，速度为 $v$ ，则 $1$ 单位时间后，有 $p_{x}$ 的概率 $v \leftarrow v + 1$ ，其余情况下 $v \leftarrow v - 1$ ，随后 $x \leftarrow x + v$ 。当 $x < 1$ 或 $x > n$ 时，随机游走终止。

这个人的初始速度总是为 $0$ 。对所有 $x \in [1, n]$ ，求初始位置为 $x$ 时，随机游走的期望持续时间。

速度每次只会加减 $1$ ，容易知道，速度的上界是 $O (\sqrt{n})$ 的。

基于此，有效状态 $(x, v)$ 只有 $O (n \sqrt{n})$ 种，暴力做高斯消元的复杂度为 $O (n^{4.5})$ 。

状态间会循环转移的原因在于速度可正可负，但是速度的正负性改变时总会经过 $0$ ，于是考虑将所有 $(x, 0)$ 视作关键状态。我们考虑 $(x, 0)$ 之间的转移，钦定转移过程中 $v \neq 0$ 。此时人总是朝单个方向移动，所以这里的转移系数可以简单的设一个 dp 进行计算，不会有循环转移的情况。

最后我们对 $O (n)$ 个关键状态高斯消元即可。

2024.6.1 展开目录

小班课展开目录

有 $n$ 个学生和 $m$ 个课程，第 $i$ 个课程最多能容纳 $b_{i}$ 个学生。第 $i$ 名学生对课程有一个优先度序列 $a_{i, 1 \dots k_{i}}$ ， $a_{i, 1}$ 优先度最高， $a_{i, k_{i}}$ 优先度最低。每名学生选课时会选择优先度最高的未满员的课程加入，若优先度序列中的所有课程都满员，该学生就不会选任何课。求一个 $1 \sim n$ 的排列使得所有学生按此顺序选课时，能选到课的学生最多。

如果不考虑优先度的问题，单纯的让尽可能多的学生去匹配一个优先度序列中的课程，这就是二分图匹配，可以用 Dinic 解决。但是网络流无法处理优先级问题。

为了处理优先级，我们想到了匈牙利算法，因为匈牙利算法对于每一个左部点的匹配策略恰好就是，按顺序枚举出边，找到第一个可以匹配的右部点并匹配上。用匈牙利求出匹配后，我们需要确定一个排列使得按此顺序选课恰好能取到我们跑出的最大匹配。

对于第 $i$ 个学生，若其匹配的课是 $a_{i, j}$ ，则所有匹配到 $a_{i, x}, x < j$ 的学生应该在 $i$ 之前选课。可以依此建一张有向图。

可以结合匈牙利的流程感性理解图中一定不会连出环。对 DAG 跑拓扑排序即可。

复杂度为 $O (n^{3})$ ，瓶颈是匈牙利。

密码展开目录

给一张 $n$ 个点的无向图 $G$ 。每次询问需要给交互库一棵包含所有点的树，交互库会返回树中有多少边在 $G$ 中也存在。

$n \leq 500, m \leq 2000$ ，询问次数 $\leq 20000$ 。

这个询问次数看起来就是 $m \log n$ 级别的，所以我们考虑用 $\log n$ 次询问来确定一条边。

很自然的考虑二分一个点的出边，这样我们需要支持查询 $u$ 是否向 $[l, r]$ 内的点有连边。我们可以连接所有 $u \to [l, r]$ 的边，但这些边构不成树，我们需要一些边将其他点和 $u$ 连通，但这些边应当不影响我们处理交互库返回的信息。

我的考场思路是考虑到 $m$ 远小于 $n^{2}$ ，如果随机一棵树，则有较大的概率其中所有边都在原图中不存在，这样就可以用这棵树内的边来将我们希望查询的边集补成树。但是，如果点 $u$ 度数较大，我们很难或者根本无法随机到一条 $u$ 的出边满足其不在 $G$ 中。可以对于度数太大的点采取一些特殊的处理方式，但总之这种做法并不优秀。

注意到我们可以用 $n$ 次询问问出一个点的所有出边。于是一种确定性的做法是，先问出 $1$ 的出边，处理其他点时，就可以用 $1$ 的出边来将所有点连通，由于我们知道 $1$ 的哪些出边在 $G$ 中，所以直接从交互库返回的信息中去掉这部分贡献即可。

2024.6.3 展开目录

FCT 展开目录

给长度为 $n$ 的序列 $A, B$ ，下标为 $[0, n)$ 。定义
$C_{i} = (\sum_{j + k = i} A_{j} B_{k} (\binom{i}{j})) mod 3$
求 $C_{0 \dots 2 n - 2}$ 。

一个经典结论是 $(\binom{n}{k}) mod 2 = 1$ 当且仅当 $k$ 是 $n$ 的子集，用 Lucas 定理易证。

模 $3$ 意义下也类似， $(\binom{n}{k}) mod 3 \neq 0$ 当且仅当 $k$ 的每个三进制位都小于等于 $n$ 。

一种做法是，考虑一共有多少对 $(n, k)$ 满足 $(\binom{n}{k}) mod 3 \neq 0$ 。这个数量应当等于 $\sum_{i = 0}^{l} 3^{i} \sum_{j = 0}^{l - i} 2^{j}$ ，其中 $l = \log_{3} n$ 。由二项式定理容易算出有值的 $(n, k)$ 只有 $6^{l}$ 对。我们可以只在有值的 $(n, k)$ 处计算 $A_{k} B_{n - k}$ 对 $C_{n}$ 的贡献，这样复杂度为 $O (6^{\log_{3} n}) = O (n^{\log_{3} 6}) = O (n^{1.63})$ 。

也可以考虑分治，将序列 $A, B$ 按下标 $mod 3$ 的值分成三个子序列，这些子序列的 $3 \times 3 = 6$ 种组合中，只有 $6$ 种组合满足 $(\binom{n mod 3}{k mod 3}) \neq 0$ ，只需要对这些子问题递归下去即可。复杂度由递推式 $T (n) = 6 T (n / 3) + O (n)$ 给出，由主定理可得复杂度同样为 $O (n^{1.63})$ 。

B 展开目录

有两个点集 $S, T$ ， $\forall u \in S, v \in T$ ， $u, v$ 之间有 $1 / 2$ 的概率存在一条边。现在随机从 $S, T$ 中各随机挑一个点，求他们之间距离的期望。不连通则距离为 $0$ 。

两个点集内部的点都完全等价，所以随机选择起点和终点的过程不重要。

为了求两点间距离的期望，我们考虑用 dp 维护一个类似 bfs 的过程。

朴素的想法是设 $f (s, i, j, k)$ ，表示现在走了 $s$ 步， $S$ 中有 $i$ 个点可达， $T$ 中有 $j$ 个点可达，上一步拓展了 $k$ 个点，到达这个当前状态的概率。最后拓展的 $k$ 个点可以用于转移，可以根据 $s$ 的奇偶性判断这个 $k$ 个点是在 $S$ 还是在 $T$ 。转移时考虑这 $k$ 个点可以到达多少原本不可达的点，如果是从 $S$ 走到 $T$ 还需要考虑是否能走到终点，若能则将 dp 值乘上对应系数贡献到答案。总复杂度 $O (n^{5})$ 。

但是容易发现这个 $s$ 只在贡献到答案时有用，我们可以直接将其去掉。重新设 $f (0 / 1, i, j, k)$ ，用 $0 / 1$ 表示现在在 $S$ 还是 $T$ ，其余状态和之前含义一致，dp 值转而维护当前状态到达终点的期望步数。但是这里存在一个问题，就是起点不一定能走到终点，所以这里的期望步数实际上只考虑了能到达终点的情况的概率乘权值之和。转移时不能简单的将期望步数 $+ 1$ ，只有能到达终点的情况步数才会 $+ 1$ ，所以还需要维护 $g (0 / 1, i, j, k)$ 表示当前状态能走到终点的概率以辅助转移。

总复杂度 $O (n^{4})$ 。

篮球大师展开目录

给一个二次函数集合，每个二次函数有定义域 $[l_{i}, + \infty)$ 。维护一个数据结构，支持向集合中插入二次函数，查询集合内所有函数在某横坐标上的最大值。

我们熟知的维护函数最值的数据结构是李超线段树，其可以支持插入一次函数和查询 $x = k$ 处的函数最值。

但是处理一次函数的方法并不能推广至二次函数，原因是两个二次函数可能有多于一个交点，在线段树上插入时中点处优的函数可能在两侧都劣，从而之前的复杂度分析不再适用。

EI 的集训队论文中介绍了一种高效的维护函数最值的方法。

首先介绍 DS 序列：记一个长为 $m$ 的序列 $σ_{1}, σ_{2}, \dots, σ_{m}$ 是 $(n, s)$ DS 序列（记作 $D S (n, s)$ ）当且仅当 $σ_{i} \in [1, n] \cap Z$ ，且对于任意 $x, y$ 交替的序列，若其为 $σ$ 的子序列，则其长度不超过 $s + 1$ 。

很容易发现 DS 序列与函数最值之间的联系。考虑对所有函数取最大值得到的分段函数，考察每一段最大值是从哪个函数上取到，这就是一个 DS 序列。而 $s$ 则代表了两个函数取最大值得到的分段函数最多会分成多少段。若不考虑定义域限制，则 $s$ 就是两个函数的最大交点个数；若对定义域进行限制，那么 $s$ 还可能再增加 $2$ 。

本题中，两个二次函数最多有两个交点，同时由于对定义域左边界有限制，所以 $s = 3$ 。

记 $λ_{s} (n)$ 表示 $D S (n, s)$ 可能的最长长度，则有结论：对任意常数 $s$ ， $λ_{s} (n)$ 都是近乎线性的（其只会携带一个和 $α (n)$ 有关的系数）。

所以，如果希望维护函数最值，只要两函数间至多有 $O (1)$ 个交点，我们可以直接维护对所有函数取最大值得到的分段函数。根据 DS 序列的性质，分段函数的段数可以被认为是线性的。

如果只需要支持查询，可以分治求出最大值的分段函数，合并两个分段函数是容易的。本题由于需要支持插入，使用二进制分组即可，总复杂度 $O (q \log^{2} n)$ ，瓶颈在查询，可以使用 Fractional Cascading 优化到单 $\log$ 。

2024.6.7 展开目录

图上删边 / CF1368E Ski Accidents 展开目录

我们只能删 $⌊ \frac{4}{7} n ⌋$ 个点。考虑一个点只有至多两条出边时图可能是什么形态，发现对于三层的完全二叉树，我们删掉所有叶子，切断所有路径的同时恰好从 $7$ 个点中删了 $4$ 个点。所以大胆设计如下算法：拓扑排序的同时对每个点维护其他点到它的最长距离，如果发现这个最长距离为 $2$ 则将它立刻删掉。容易证明这个算法是正确的。核心在于上面这个删掉所有叶子的操作保证了剩下的 $3$ 个点不会对原图其他部分有任何影响，所以我们可以把图划分成若干个不超过 $3$ 层的 DAG，这些局部间互不影响，每个 DAG 都只会删不超过 $4 / 7$ 个点。

启发是，构造题若不需要最优化操作次数，则可以考虑在可以接受的范围内通过更多的操作使整体有更优的性质。

2024.6.8 展开目录

想不出展开目录

在平面上给定 $n$ 个点，第 $i$ 个点的坐标为 $(i, p_{i})$ ，其中 $p$ 是 $1 \sim n$ 的排列。从每个点引出一条向上或向右的射线，问这些射线最多能将平面分成多少个有界区域。

若将无界区域也算进答案，那么由欧拉公式或直接观察可得，区域数应当为所有射线的交点个数 $+ 1$ 。无界区域的个数仅和射线形成的连通块个数有关，我们只需考虑最大化交点个数，此时连通块个数也一定取到了最小值。

一种符合直觉的射线定向方案是，若点左上方的点比右下方的点多，则连向上的射线，否则取向下的射线。考场上我只是证明了在这样的定向方案下，每个点连出的射线上的交点一定超过左上方点与右下方点数量总和的一半，但是这个证明不够严谨。

一个关键结论是，若一个点 $A$ 在另一个点 $B$ 的左上角，则 $A$ 的射线向右， $B$ 的射线向上。若不然，交换两点的射线方向一定严格优（至少新增一个交点）。

于是回到之前猜测的基于贪心的定向方案。不妨设点 $A$ 左上方的点比右下方的点多，若 $A$ 的射线向右，则左上方的点的射线全部向右，此时将 $A$ 的射线方向改为向上一定不劣。这样就证明了定向方案的正确性。

于是我们可以用二维数点统计答案。复杂度 $O (n \log n)$ 。

题解还有一种人类智慧的答案统计方法。对于所有射线向上的点 $A (i, p_{i})$ ，设其左上方点个数为 $x$ ，右下方点个数为 $y$ ，我们知道 $x \geq y$ 。假设左上方的点射线全部向右，这样就产生了 $x$ 个交点。但是对于右下方的点而言，他们的射线方向也都向上，同时都会假设 $A$ 向右，这样就多算了 $y$ 的贡献。于是总贡献为 $x - y$ ，射线向右时贡献为 $y - x$ ，可以简单的合并为 $| x - y |$ 。将 $x, y$ 同时加上 $A$ 左下角的点数，可以进一步简化为 $| i - p_{i} |$ 。总交点个数即为 $(\sum | i - p_{i} |) / 2$ 。

2024.6.11 展开目录

虚无展开目录

给定长度为 $n$ 的 01 序列 $a$ 。对每个 $k \in [1, n]$ ，求将 $a$ 划分为 $k$ 个子段再按任意顺序重新拼接后，新序列中最长不下降子序列的最大长度。

01 序列上的不下降子序列形如前面一部分是 0，剩余部分是 1。所以对于 $a$ 划分出的 $k$ 个子段，只会有不超过一个子段贡献前缀中的 $0$ ，剩余后缀中的 $1$ ，剩余段要么贡献 $0$ ，要么贡献 $1$ 。

可以将特殊的段一分为二，将问题改为划分 $k + 1$ 个子段，每个子段只贡献 $0$ 或 $1$ 。由于所有子段选取的数一定是 01 交替的（否则可以将两段合并），所以 $k > 1$ 时总存在相邻两段，前者取 $0$ ，后者取 $1$ ，将这两段合并即可。 $k = 1$ 的情况平凡，特殊处理即可。

可以将 $0$ 和 $1$ 的连续段合并，那么选 $k$ 个子段，每个子段贡献 $0$ 或 $1$ 可以转化为删掉若干个不相邻的连续段。删一个连续段代表这个段对答案不作贡献，同时左右两侧的连续段合并，可以选在同一个子段内对答案做贡献。这是经典的模拟费用流问题（LG1484 种树），用堆解决即可。

费用流模型参考：

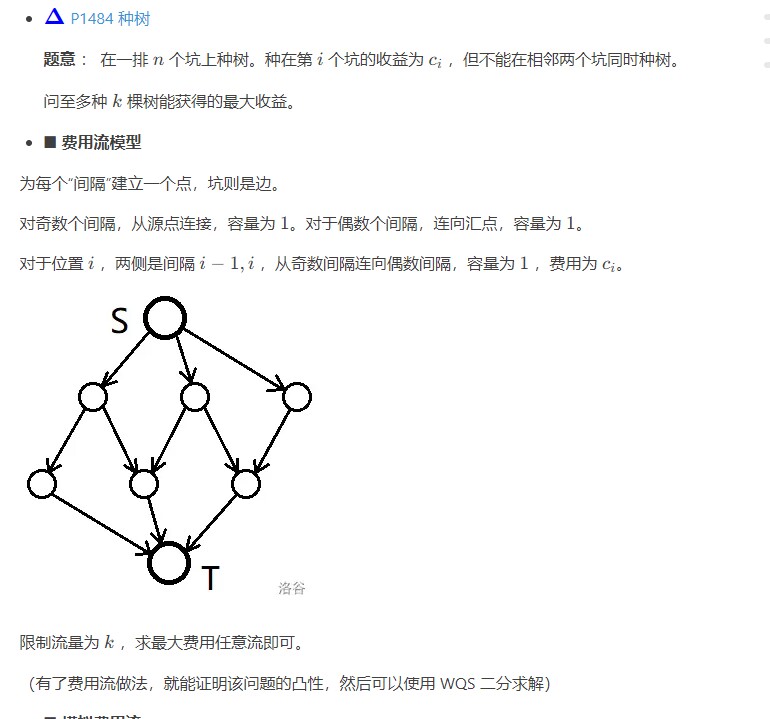
也可以直接观察出答案在 $k$ 为奇数和偶数时分别是凸的。同时若分别对序列的两部分求出分 $k$ 段的最优答案，合并时做的是 $(max, +)$ 卷积。分治然后用 Minkowski 和合并 dp 数组即可。

两种做法复杂度均为 $O (n \log n)$ 。

2024.6.14 展开目录

装甲方阵 / CF1427G One Billion Shades of Grey 展开目录

直接处理绝对值通常是困难的，一种常见的处理方式是，如果我们要最大化某个绝对值，可以直接将绝对值拆开枚举符号。但是本题中这种方法显然无法使用。

本题中要对多个绝对值求和，我们考虑拆贡献。可以将 $| x - y |$ 看作是 $x$ 到 $y$ 的距离，然后将贡献拆到每个单位长度上。具体来说就是枚举 $k$ ，求 $\sum [(x \leq k \land y > k) \lor (y \leq k \land x > k)]$ ，然后对这个值求和。而对于某特定 $k$ ，上述和式容易使用最小割刻画，也就是若 $x, y$ 被划分入不同集合则产生 $1$ 的代价，这只需在 $x, y$ 间连双向边即可。

枚举 $k$ 时网络流的图会发生改变，每次重跑最大流开销太大。但是由于加边和删边的操作一共只有 $O (n^{2})$ 次，删边时手动退流即可，加边则可以直接在残量网络上跑最大流。所谓退流就是对 $u \to S, T \to v$ 分别求最大流。暂时不懂退流复杂度，只知道如果朴素的使用 dinic 退流，bfs 时搜到汇点就立刻退出会对运行效率有显著提升。

装甲会战 / TopCoder14379 RPSRobots 展开目录

刘一平老师在 WC 讲的题。

石头剪刀布可以用三进制减法刻画。然后有聪明人想到了用三次单位根来描述这个三进制除法，这样，我们还可以通过 $ω_{3}^{0}, ω_{3}^{1}, ω_{3}^{2}$ 的线性组合描述「胜 / 平 / 负」的场数。

我们希望两个机器人的策略序列无论如何循环移位，用对应位置进行游戏后，结果中的胜平负场次都相同。循环移位后用对应位置进行游戏可以用循环差卷积刻画，或者也就是将某个序列反转后做循环卷积，我们希望的就是卷积结果的每一位都相同。

做循环卷积是困难的。一个关键的事实是，做长度为 $n$ 的 DFT 就是在做长度为 $n$ 的循环卷积。这是因为如果带入 $ω_{n}^{k}$ 求点值， $x^{i} = ω_{n}^{i k}$ 和 $x^{n + i} = ω_{n}^{i n + i k}$ 其实是相等的。由于 $n$ 个点值唯一确定了一个 $n - 1$ 次多项式，我们说明循环卷积的结果能够对应所有点值，就说明了 DFT 求出的结果就是循环卷积。平时的循环卷积不使用 DFT 是因为 FFT 只能用在长度为 $2^{k}$ 的序列上。